题目内容
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名歌手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(Ⅱ) X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
解:(Ⅰ) 设事件A 表示:观众甲选中3号歌手且观众乙未选中3号歌手.
观众甲选中3号歌手的概率为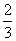 ,观众乙未选中3号歌手的概率为
,观众乙未选中3号歌手的概率为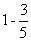 .
.
所以P(A) = 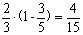 .
.
因此,观众甲选中3号歌手且观众乙未选中3号歌手的概率为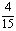
(Ⅱ) X表示3号歌手得到观众甲、乙、丙的票数之和,则X可取0,1,2,3.
观众甲选中3号歌手的概率为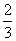 ,观众乙选中3号歌手的概率为
,观众乙选中3号歌手的概率为 .
.
当观众甲、乙、丙均未选中3号歌手时,这时X=0,P(X = 0) = 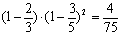 .
.
当观众甲、乙、丙中只有1人选中3号歌手时,这时X=1,P(X = 1) = 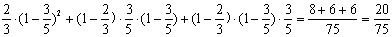 .
.
当观众甲、乙、丙中只有2人选中3号歌手时,这时X=2,P(X = 2) = 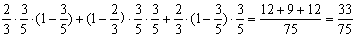 .
.
当观众甲、乙、丙均选中3号歌手时,这时X=3,P(X =3) = 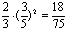 .
.
X的分布列如下表:
| X | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
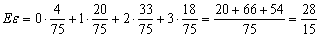
所以,数学期望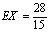

练习册系列答案
相关题目
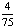
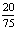
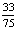
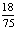
 , 则
, 则 =( )
=( )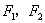 分别为双曲线
分别为双曲线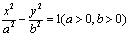 的左、右焦点,双曲线上存在一点
的左、右焦点,双曲线上存在一点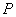 使得
使得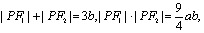 则该双曲线的离心率为( )
则该双曲线的离心率为( ) B.
B.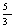 C.
C. D.3
D.3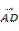 ·
·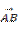 =
= ,则
,则 表示的平面区域是( )
表示的平面区域是( )
 的图象大致是( )
的图象大致是( )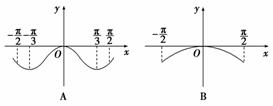

 等于( )
等于( )