题目内容
已知f(n)=sin
,n∈Z.
(1)求证:f(1)+f(2)+…+f(8)=f(9)+f(10)+…+f(16);
(2)求f(1)+f(2)+…+f(2013)的值.
| nπ |
| 4 |
(1)求证:f(1)+f(2)+…+f(8)=f(9)+f(10)+…+f(16);
(2)求f(1)+f(2)+…+f(2013)的值.
考点:数列的求和
专题:计算题,函数的性质及应用,三角函数的求值
分析:(1)f(n)=sin
为周期函数,且T=
=8,即有f(n+8)=f(n),即可得证;
(2)求出f(1),f(2),…f(8)的值,再由周期8,算出2013项中周期的个数,即可计算.
| nπ |
| 4 |
| 2π | ||
|
(2)求出f(1),f(2),…f(8)的值,再由周期8,算出2013项中周期的个数,即可计算.
解答:
(1)证明:f(n)=sin
为周期函数,且T=
=8,即有f(n+8)=f(n),
则f(9)=f(1),f(10)=f(2),…,f(16)=f(8),
则有f(1)+f(2)+…+f(8)=f(9)+f(10)+…+f(16);
(2)解:由于f(1)=
,f(2)=sin
=1,f(3)=sin
=
,f(4)=sinπ=0,
f(5)=sin
=-
,f(6)=sin
=-1,f(7)=sin
=-
,f(8)=sin2π=0.
则f(1)+f(2)+…+f(8)=0,
且2013=8×251+5,
则f(1)+f(2)+…+f(2013)=f(1)+f(2)+…+f(5)=1+
.
| nπ |
| 4 |
| 2π | ||
|
则f(9)=f(1),f(10)=f(2),…,f(16)=f(8),
则有f(1)+f(2)+…+f(8)=f(9)+f(10)+…+f(16);
(2)解:由于f(1)=
| ||
| 2 |
| π |
| 2 |
| 3π |
| 4 |
| ||
| 2 |
f(5)=sin
| 5π |
| 4 |
| ||
| 2 |
| 3π |
| 2 |
| 7π |
| 4 |
| ||
| 2 |
则f(1)+f(2)+…+f(8)=0,
且2013=8×251+5,
则f(1)+f(2)+…+f(2013)=f(1)+f(2)+…+f(5)=1+
| ||
| 2 |
点评:本题考查函数的周期性及运用,考查三角函数的求值,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过圆x2+y2-6x-8y+21=0上一动点P作圆x2+y2=4的两条切线,切点分别为A、B,设向量
、
的夹角为θ,则cosθ的取值范围为( )
| PA |
| PB |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
以下表示正确的是( )
| A、∅=0 | B、∅={0} |
| C、∅∈{0} | D、∅⊆{0} |
已知{an},{bn}均为等差数列,且a2=8,a6=16,b2=4,b6=a6,则由{an},{bn}的公共项组成的新数列{cn}的通项公式cn等于( )
| A、3n+4 | B、6n+2 |
| C、6n+4 | D、2n+2 |
 如图为函数f(x)=
如图为函数f(x)=| 2x |
| x2+1 |
| A、π | B、2π | C、3π | D、4π |
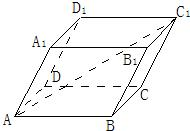 如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.
如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.