题目内容
1.求函数y=$\frac{sinx+1}{2sinx-1}$的值域.分析 分离常数,借助三角函数的有界性求解.
解答 解:y=$\frac{sinx+1}{2sinx-1}$=$\frac{2(sinx+1)}{2(2sinx-1)}$=$\frac{1}{2}$+$\frac{3}{4sinx-2}$,
∵-1≤sinx≤1,
∴-6≤4sinx-2<0,或0<4sinx-2≤2,
∴$\frac{3}{4sinx-2}$≤-$\frac{1}{2}$,或$\frac{3}{4sinx-2}$≥$\frac{3}{2}$,
∴$\frac{1}{2}$+$\frac{3}{4sinx-2}$≤0,或$\frac{1}{2}$+$\frac{3}{4sinx-2}$≥2,
∴函数y=$\frac{sinx+1}{2sinx-1}$的值域为:(-∞,0]∪[2,+∞).
点评 本题考查三角函数的最值,考查正弦函数的有界性,考查转化与方程思想,属于中档题.

练习册系列答案
相关题目
12.已知抛物线的顶点在坐标原点,焦点是圆(x-3)2+y2=4的圆心,则抛物线的方程是( )
| A. | x2=12y | B. | x2=6y | C. | y2=12x | D. | y2=6x |
9.执行下图的程序框图,若输入的a,b,k分别是2,1,3,则输出的M=( )
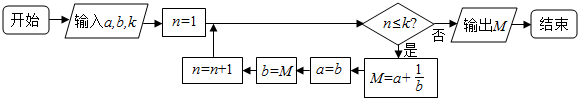
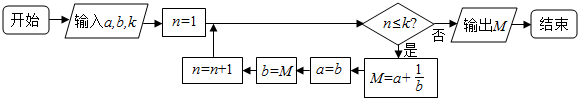
| A. | $\frac{4}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
16.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,Q为右支上一点,P点在直线x=-a上,且满足$\overrightarrow{PQ}$=$\overrightarrow{Q{F}_{2}}$,$\overrightarrow{OQ}$=λ($\frac{\overrightarrow{O{F}_{2}}}{|\overrightarrow{O{F}_{2}}|}$+$\frac{\overrightarrow{OP}}{|\overrightarrow{OP}|}$)(λ≠0),则该双曲线的离心率为( )
| A. | $\sqrt{5}$+1 | B. | $\sqrt{2}$+1 | C. | 2 | D. | $\sqrt{2}$ |
2.已知函数f(x)=asinx-bcosx(a、b为常数,a≠0,x∈R)在x=$\frac{π}{4}$处取得最小值,则函数y=|f($\frac{3π}{4}$-x)|是( )
| A. | 最大值为$\sqrt{2}$b且它的图象关于点(π,0)对称 | |
| B. | 最大值为$\sqrt{2}$a且它的图象关于点($\frac{3π}{4}$,0)对称 | |
| C. | 最大值为$\sqrt{2}$b且它的图象关于直线x=π对称 | |
| D. | 最大值为$\sqrt{2}$a且它的图象关于直线x=$\frac{3π}{4}$对称. |