题目内容
10.化简下列算式(1)lg5•lg20+(lg2)2
(2)${({-\frac{27}{8}})^{-\frac{2}{3}}}+{(0.002)^{-\frac{1}{2}}}-10{({\sqrt{5}-2})^{-1}}+{({\sqrt{2}-\sqrt{3}})^0}$.
分析 (1)根据对数的运算性质化简即可,
(2)根据指数幂的运算性质化简即可.
解答 解:(1)原式=lg5(lg4+lg5)+(lg2)2=(lg5+lg2)2=1,
(2)原式=(-$\frac{3}{2}$)${\;}^{3×(-\frac{2}{3})}$+(2×10-3)${\;}^{{\;}^{\;}}$${\;}^{-\frac{1}{2}}$-$\frac{10}{\sqrt{5}-2}$+1=$\frac{4}{9}$+10$\sqrt{5}$-10($\sqrt{5}$+2)+1=-$\frac{167}{9}$
点评 本题考查了指数幂和对数的运算性质,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5.某商店将进价每个10元的商品按每个18元售出时,每天可卖出60个,商店经理到市场上做了一番调查后发现,若将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;若将这种商品的售价(在每个18元的基础上)每降低1元,则日销售量增加10个.为了每日获得最大利润,则商品的售价应定为( )
| A. | 10元 | B. | 15元 | C. | 20元 | D. | 25元 |
19.已知全集U={x∈N+|-2<x<9},M=(3,4,5),P={1,3,6},那么{2,7,8}是( )
| A. | M∪P | B. | M∩P | C. | (∁UM)∪(∁∪P) | D. | (∁UM)∩(∁UP) |
20.下列函数在(0,+∞)上为减函数的是( )
| A. | y=-|x-1| | B. | y=x2-2x+3 | C. | y=ln(x+1) | D. | y=2${\;}^{-\frac{x}{2}}$ |
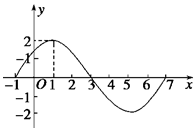 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.