题目内容
已知向量
,
满足|
|=3,|
|=2
,且
⊥(
+
),则向量
与
的夹角是( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
| A、90° | B、120° |
| C、135° | D、150° |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算性质即可得出.
解答:
解:∵
⊥(
+
),
∴
•(
+
)=
2+
•
=|
|2+|
||
|cos<
,
>=0,
又满足|
|=3,|
|=2
,
∴32+3×2
cos<
,
>=0,
解得cos<
,
>=-
.
∴<
,
>=150°.
故选:D.
| a |
| a |
| b |
∴
| a |
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
又满足|
| a |
| b |
| 3 |
∴32+3×2
| 3 |
| a |
| b |
解得cos<
| a |
| b |
| ||
| 2 |
∴<
| a |
| b |
故选:D.
点评:本题考查了向量的数量积运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
定义在(-1,1)上的函数f(x)-f(y)=f(
);当x∈(-1,0)时f(x)>0.若P=f(
)+f(
),Q=f(
),R=f(0);则P,Q,R的大小关系为( )
| x-y |
| 1-xy |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 2 |
| A、P<Q<R |
| B、R<Q<P |
| C、R<P<Q |
| D、Q<P<R |
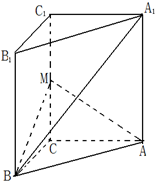 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A=