题目内容
设数列{an}满足:a1=2,an+1=
,证明:对?n∈N*,有2≤an<an+1<3.
| 3+4an |
| 2+an |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得an+1+1=
,an+1-3=
,从而
=5×
,又
=-3,进而
=-3×5n-1,由此得到an=
,an+1-an=
-
=
>0,从而能证明对?n∈N*,有2≤an<an+1<3
| 5+5an |
| 2+an |
| an-3 |
| 2+an |
| an+1+1 |
| an+1-3 |
| an+1 |
| an-3 |
| a1+1 |
| a1-3 |
| an+1 |
| an-3 |
| 9×5n-1-1 |
| 3×5n-1+1 |
| 9×5n-1 |
| 3×5n+1 |
| 9×5n-1-1 |
| 3×5n-1+1 |
| 12(5n-5n-1) |
| (3×5n+1)(3×5n-1+1) |
解答:
解:∵数列{an}满足:a1=2,an+1=
,
∴an+1+1=
+1=
,
an+1-3=
-3=
,
∴
=5×
,又
=-3,
∴{
}是首项为-3,公比为5的等比数列,
∴
=-3×5n-1,
解得an=
,
∴an+1-an=
-
=
=
>0,
∴数列{an}是增数列,∴{an}min=a1=2,
∴an+1=
=4-
<4-
<3,
∴对?n∈N*,有2≤an<an+1<3.
| 3+4an |
| 2+an |
∴an+1+1=
| 3+4an |
| 2+an |
| 5+5an |
| 2+an |
an+1-3=
| 3+4an |
| 2+an |
| an-3 |
| 2+an |
∴
| an+1+1 |
| an+1-3 |
| an+1 |
| an-3 |
| a1+1 |
| a1-3 |
∴{
| an+1 |
| an-3 |
∴
| an+1 |
| an-3 |
解得an=
| 9×5n-1-1 |
| 3×5n-1+1 |
∴an+1-an=
| 9×5n-1 |
| 3×5n+1 |
| 9×5n-1-1 |
| 3×5n-1+1 |
=
| (9×5n-1)(3×5n-1+1)-(9×5n-1-1)(3×5n+1) |
| (3×5n+1)(3×5n-1+1) |
=
| 12(5n-5n-1) |
| (3×5n+1)(3×5n-1+1) |
∴数列{an}是增数列,∴{an}min=a1=2,
∴an+1=
| 3+4an |
| 2+an |
| 5 |
| 2+an |
| 5 |
| 2+2 |
∴对?n∈N*,有2≤an<an+1<3.
点评:本题考查不等式的证明,综合性强,难度大,对数学思维要求较高,解题的关键是构造出{
}是首项为-3,公比为5的等比数列.
| an+1 |
| an-3 |

练习册系列答案
相关题目
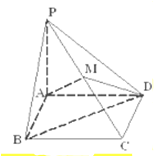 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,点M是棱PC的中点,AM⊥平面PBD
(1)求四棱锥P-ABCD的体积;
(2)求平面PAD与平面AMD所成二面角的大小.
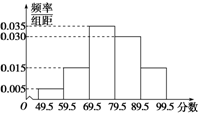 某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )
某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )| A、18篇 | B、24篇 |
| C、25篇 | D、27篇 |
已知向量
,
满足|
|=3,|
|=2
,且
⊥(
+
),则向量
与
的夹角是( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
| A、90° | B、120° |
| C、135° | D、150° |