题目内容
已知非零向量
,
满足|
|=1,且
与
-
的夹角为30°,则|
|的取值范围是( )
| a |
| b |
| b |
| b |
| b |
| a |
| a |
A、(0,
| ||
B、[
| ||
| C、[1,+∞) | ||
D、[
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:在空间任取一点C,分别作
=
,
=
,则
=
-
,并且使∠A=30°.从而
,
,
-
便构成一个三角形,从三角形中,便能求出|
|的取值范围.
| CB |
| a |
| CA |
| b |
| BA |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
解答:
 解:根据题意,作
解:根据题意,作
=
,
=
;
∴
-
=
,且∠A=30°;
过C作CD⊥AB,垂足为D,则CD的长度便是|
|的最小值;
在Rt△CDA中,CA=1,∠A=30°,∴CD=
;
∴|
|的取值范围是[
,+∞).
故选D.
 解:根据题意,作
解:根据题意,作| CB |
| a |
| CA |
| b |
∴
| b |
| a |
| BA |
过C作CD⊥AB,垂足为D,则CD的长度便是|
| a |
在Rt△CDA中,CA=1,∠A=30°,∴CD=
| 1 |
| 2 |
∴|
| a |
| 1 |
| 2 |
故选D.
点评:把
,
,
-
这三个向量放在一个三角形中,是求解本题的关键.
| a |
| b |
| b |
| a |

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
正方形ABCD的边长为1,则|
+
|为( )
| AB |
| AD |
| A、1 | ||
B、
| ||
| C、3 | ||
D、2
|
下列空间几何体能较合适作为平面等边三角形的类比对象的是( )
| A、正四棱锥 | B、正方体 |
| C、正四面体 | D、球 |
设
=(cosα,sinα),
=(cosα,1-
),若
⊥
,则锐角α为( )
| a |
| b |
| 5 |
| 4sinα |
| a |
| b |
| A、15° | B、30° |
| C、45° | D、60° |
设等边三角形的边长为a,P是△ABC内的任意一点,且P到三边AB、BC、CA的距离分别为d1、d2、d3,则有d1+d2+d3为定值
a,由以上平面图形的特性类比空间图形:设正四面体ABCD的棱长为a,P是正四面体ABCD内任意一点,即到四个面ABC,ABD,ACD,BCD的距离分别为d1、d2、d3、d4,则有d1+d2+d3+d4为定值( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设命题p:命题“?x∈R,x2+x+1=0”的否定是“?x∈R,x2+x+1≠0”;命题q:“x>2”是“|x-1|>1”的充分不必要条件,则( )
| A、“p或q”为真 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p,q均为假命题 |
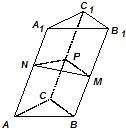 类比正弦定理,如图,在三棱柱ABC-A1B1C1中,二面角B-AA1-C、C-BB1-A、B-CC1-A,所成的平面角分别为α、β、γ,则有
类比正弦定理,如图,在三棱柱ABC-A1B1C1中,二面角B-AA1-C、C-BB1-A、B-CC1-A,所成的平面角分别为α、β、γ,则有