题目内容
11.在平面直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(l为参数,α为直线l的倾斜角).以原点为极点,x轴的非负半轴为极轴建立极坐标系,并在两个坐标系下取相同的长度单位.(Ⅰ)当α=$\frac{π}{4}$时,求直线l的极坐标方程;
(Ⅱ)若曲线C和直线l交于M,N两点,且|MN|=$\sqrt{15}$,求直线l的倾斜角.
分析 (I)由$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$,消去参数t可得:x-y-1=0,利用互化公式可得极坐标方程.
(II)由曲线C的参数方程为$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),消去参数θ可得普通方程.将直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(l为参数,代入圆的方程:t2-2tcosα-3=0,利用|MN|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{15}$,代入解出即可的.
解答 解:(I)由$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$,消去参数t可得:x-y-1=0,可得极坐标方程:ρcosθ-ρsinθ-1=0,即$\sqrt{2}ρcos(θ+\frac{π}{4})$=1.
(II)由曲线C的参数方程为$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),消去参数θ可得:(x-2)2+y2=4.
将直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(l为参数,代入圆的方程:t2-2tcosα-3=0,△>0.
则t1+t2=2cosα,t1•t2=-3,|MN|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{4co{s}^{2}α+12}$=$\sqrt{15}$,
cosα=±$\frac{\sqrt{3}}{2}$.∴α=$\frac{π}{6}$或$\frac{5π}{6}$.∴直线l的倾斜角为$\frac{π}{6}$或$\frac{5π}{6}$.
点评 本题考查了极坐标方程化为直角坐标方程、直线的参数方程及其应用、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1(x>3) | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1(x<-7) | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y>3) | D. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{7}$=1(y<-3) |
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 6 |
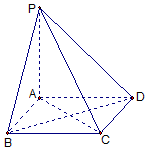 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.