题目内容
16.设向量$\overrightarrow a=(1,2),\overrightarrow b=(2,3)$,若向量$λ\overrightarrow a+\overrightarrow b$与向量$\overrightarrow c=(-4,-7)$垂直,则λ=$-\frac{29}{18}$.分析 先求出向量$λ\overrightarrow{a}+\overrightarrow{b}$的坐标,根据$λ\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{c}$垂直,从而有$(λ\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{c}=0$,进行数量积的坐标运算便可得到关于λ的方程,解出λ即可.
解答 解:$λ\overrightarrow{a}+\overrightarrow{b}=λ(1,2)+(2,3)=(λ+2,2λ+3)$;
∵向量$λ\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{c}$=(-4,-7)垂直;
∴$(λ\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{c}=-4(λ+2)-7(2λ+3)=0$;
解得$λ=-\frac{29}{18}$.
故答案为:$-\frac{29}{18}$.
点评 考查向量坐标的数乘和加法运算,向量垂直的充要条件,以及向量数量积的坐标运算.

练习册系列答案
相关题目
7.如图,在正方体ABCD-A′B′C′D′中,E为A′C′的中点,则异面直线CE与BD所成的角为( )
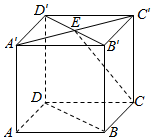

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
4.设等差数列{an}的前项和为Sn,若a1=-40,a6+a10=-10,则当Sn取得最小值时n的值为( )
| A. | 8或9 | B. | 9或10 | C. | 8 | D. | 9 |
11.函数$y={log_{\frac{1}{4}}}({-{x^2}+2x+3})$的单调增区间是( )
| A. | (-1,1] | B. | (-∞,1) | C. | [1,3) | D. | (1,+∞) |
1.若角α的终边上有一点P(0,3),则下列式子无意义的是( )
| A. | tanα | B. | sinα | C. | cosα | D. | sinαcosα |