题目内容
15.椭圆$\sqrt{{{({x-2})}^2}+{y^2}}+\sqrt{{{({x+2})}^2}+{y^2}}=6$的短轴长是2$\sqrt{5}$.分析 确定椭圆中的几何量,即可得出结论.
解答 解:$\sqrt{{{({x-2})}^2}+{y^2}}+\sqrt{{{({x+2})}^2}+{y^2}}=6$表示(x,y)到(2,0),(-2,0)的距离和为6,
∴c=2,a=3,
∴b=$\sqrt{5}$,
∴椭圆$\sqrt{{{({x-2})}^2}+{y^2}}+\sqrt{{{({x+2})}^2}+{y^2}}=6$的短轴长是2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查圆锥曲线的定义,考查方程的几何意义,考查椭圆的几何性质,是个简单题.

练习册系列答案
相关题目
5.下列函数中,既是奇函数又是周期为π的周期函数的是( )
| A. | y=|tanx| | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=cos2x | D. | y=sinxcosx |
6.在正项等比数列{an}中,10a1,$\frac{1}{2}{a_3},3{a_2}$成等差数列,则$\frac{{{a_8}+{a_{10}}+{a_{11}}}}{{{a_6}+{a_8}+{a_9}}}$=( )
| A. | 5 | B. | 4 | C. | 25 | D. | 4或25 |
3.已知f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x}&{x≥0}\\{-a{x}^{2}+x}&{x<0}\end{array}\right.$,当x∈[-$\frac{1}{4}$,$\frac{1}{4}$]时恒有f(x+a)<f(x),则实数a的取值范围是( )
| A. | ($\frac{1-\sqrt{17}}{4},0$) | B. | [-2,0) | C. | (-∞,-$\sqrt{2}$) | D. | [-2,-$\sqrt{2}$] |
20.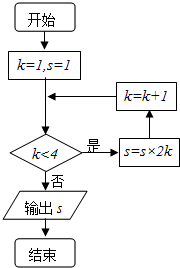 执行如图所示的程序框图,输出的s值为( )
执行如图所示的程序框图,输出的s值为( )
 执行如图所示的程序框图,输出的s值为( )
执行如图所示的程序框图,输出的s值为( )| A. | 8 | B. | 16 | C. | 48 | D. | 64 |