题目内容
7.设奇函数f(x)在(0,+∞)上为减函数,且f(2)=0,则使$\frac{{f(x)-f({-x})}}{x}>0$的x的取值范围为(-2,0)∪(0,2).分析 利用已知函数当x>0时的单调性和奇函数的对称性画出图象即可解出.
解答 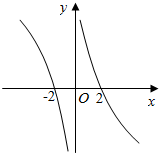 解:由f(x)在(0,+∞)上是减函数,且2是函数f(x)的一个零点,可以画出图象,
解:由f(x)在(0,+∞)上是减函数,且2是函数f(x)的一个零点,可以画出图象,
已知f(x)是定义在R上的奇函数,因此其图象关于原点对称,且f(0)=0,据此画出图象.
①当x>0时,∵$\frac{{f(x)-f({-x})}}{x}>0$,∴f(x)>0,因此0<x<2;
②当x<0时,∵$\frac{{f(x)-f({-x})}}{x}>0$,∴f(x)<0,因此-2<x<0.
综上可知:满足$\frac{{f(x)-f({-x})}}{x}>0$的x的取值范围是(-2,0)∪(0,2).
故答案为(-2,0)∪(0,2).
点评 熟练掌握奇函数的对称性和分类讨论的思想方法是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
12.已知集合A={x|x2-1=0},则下列式子表示错误的是( )
| A. | 1∈A | B. | {1}∈A | C. | ∅⊆A | D. | {1,-1}⊆A |
19.下列各组函数中,表示同一个函数的是( )
| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=x,g(x)=\sqrt{x^2}$ | ||
| C. | $f(x)=\frac{{{x^2}-9}}{x-3},g(x)=x+3$ | D. | f(x)=x2+1,g(t)=t2+1 |
17.复数$\frac{15}{2i-1}$的共轭复数是( )
| A. | 3-6i | B. | -3-6i | C. | 3+6i | D. | -3+6i |
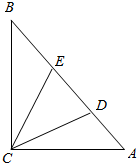 如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.
如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.