题目内容
6．已知α∩β=l，m是平面α内的任意直线，在平面β内总存在一条直线n，使下列命题一定正确的是（ ）| A． | m与n相交 | B． | m与n平行 | C． | m与n垂直 | D． | l与m、n都异面 |
分析 在A中，当直线m∥l时，m与n没有交点；在B中，当m∩l=A时，m与n不能平行；在C中，α∩β=l，m是平面α内的任意直线，在平面β内总存在一条直线n，使m与n垂直；在D中，当m∩l=A时或直线m∥l时，l与m共面．
解答 解：α∩β=l，m是平面α内的任意直线，在平面β内总存在一条直线n，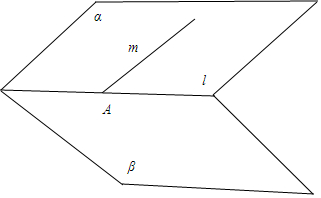
在A中，当直线m∥l时，m与n没有交点，故A错误；
在B中，如图，当m∩l=A时，m与n不能平行，故B错误；
在C中，α∩β=l，m是平面α内的任意直线，在平面β内总存在一条直线n，使m与n垂直，故C正确；
在D中，如图，当m∩l=A时或直线m∥l时，l与m共面，故D错误．
故选：C．
点评 本题考查命题真假的判断，考查空间中线线、线面、面面间的关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在四棱锥P-ABCD中，AB=BC=CD=DA，∠BAD=60°，AQ=QD，△PAD是正三角形．
17．已知椭圆C1：$\frac{{x}^{2}}{5}$+y2=1与双曲线C2的公共焦点为F1，F2，A，B分别为C1，C2在第二、第四象限的公共点．若四边形AF1BF2为矩形，则C2的离心率是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{\sqrt{6}}{2}$ |
11．设变量x，y满足约束条件$\left\{\begin{array}{l}{y≤x+1}\\{y≥2x-4}\\{x+2y≥2}\end{array}\right.$，则目标函数z=3x-2y的最大值为（ ）
| A． | 6 | B． | 3 | C． | 9 | D． | 2 |
18．在等腰直角△ABC中，P为平面ABC内的一点，斜边AB=4，则$\overrightarrow{PC}•（\overrightarrow{PA}+\overrightarrow{PB}）$的最小值是（ ）
| A． | $-\frac{8}{9}$ | B． | -1 | C． | -2 | D． | $-\frac{16}{9}$ |
15．函数$f（x）=\sqrt{{2^x}-4}$的定义域（ ）
| A． | （-∞，2] | B． | [0，2] | C． | （2，+∞） | D． | [2，+∞） |
根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图．