题目内容
如图,弧![]() 为半圆,AB为半圆直径,O为半圆圆心,且
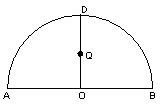
为半圆,AB为半圆直径,O为半圆圆心,且![]() ,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变。
,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变。
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过点B的直线![]() 与曲线C交于M、N两点,与OD所在直线交于E点,若
与曲线C交于M、N两点,与OD所在直线交于E点,若![]() 为定值。
为定值。
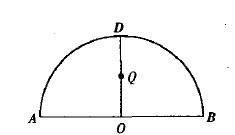
20. 解:(Ⅰ)以AB、OD所在直线分别为x轴、y轴,
O为原点,建立平面直角坐标系,
∵动点P在曲线C上运动且保持|PA|+|PB|的值不变.
且点Q在曲线C上,
∴|PA|+|PB|=|QA|+|QB|=2![]() >|AB|=4. ………………………3分
>|AB|=4. ………………………3分
∴曲线C是为以原点为中心,A、B为焦点的椭圆
设其长半轴为a, 短半轴为b, 半焦距为c, 则2a=2![]() , ∴a=
, ∴a=![]() , c=2, b=1.
, c=2, b=1.
∴曲线C的方程为![]() +y2=1 …………………………………………6分
+y2=1 …………………………………………6分
证明:(Ⅱ)设![]() 点的坐标分别为
点的坐标分别为![]() ,
,
又易知![]() 点的坐标为
点的坐标为![]() .且点B在椭圆C内, 故过点B的直线l必与椭圆C相交.
.且点B在椭圆C内, 故过点B的直线l必与椭圆C相交.
∵![]() , ∴
, ∴![]() .
.
∴ ![]() ,
,![]() . …………………………………………8分
. …………………………………………8分
将M点坐标代入到椭圆方程中得:![]() ,
,
去分母整理,得![]() . ………………………………………10分
. ………………………………………10分
同理,由![]() 可得:
可得:![]() . ………………………12分
. ………………………12分
∴ ![]() ,
,![]() 是方程
是方程![]() 的两个根, ∴
的两个根, ∴ ![]() .………14分
.………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
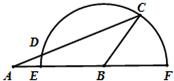 如图,在△ABC中,AB=2,
如图,在△ABC中,AB=2,
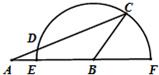 如图,在△ABC中,AB=2,
如图,在△ABC中,AB=2,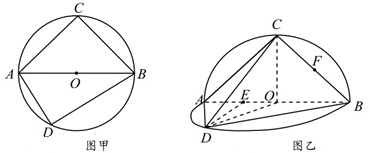
 (2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设