Question

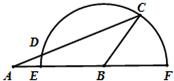如图，在△ABC中，AB=2，BC=

2

，∠ABC=

3π

4

．以点B为圆心，线段BC的长为半径的半圆分别交AB所在直线于点E、F，交线段AC于点D，求弧

CD

的长．（精确到0.01）

Answer 1

分析：方法一：用余弦定理与正弦定理依次求出线段AC的长与角ACB的大小，进而在三角形DBC中求弧

CD

的所对的圆心角的大小，用弧长公式求出弧长．
方法二：建立坐标系，求出线段BD与线段BC所对应的向量的坐标，然后用向量的夹角公式算出角DBC的大小，再用弧长公式求出弧长．

解答：解：
解法一：连接BD，在△ABC中，由余弦定理得
AC²=AB²+BC²-2•AB•BC•cos∠ABC=4+2-4

2

•(-

2

2

)=10
所以AC=

10

．
再由正弦定理得

AC

sin∠ABC

=

AB

sin∠ACB

?sin∠ACB=

2• 2 2

10

=

5

5

在△DBC中，因为BD=BC，故∠DBC=π-2arcsin

5

5

，
所以

CD

=(π-2arcsin

5

5

)•

2

≈3.13．
解法二：如图，以点B为坐标原点，AB所在的直线为x轴建立平面直角坐标系，
由条件可得点A的坐标为（-2，0），点C的坐标为（1，1），
故直线AC的方程为y=

1

3

(x+2)，
和圆方程x²+y²=2联立得

x2+y2=2 y= 1 3 (x+2)

可解得x=-

7

5

和x=1，即得点D的坐标为(-

7

5

，

1

5

)．
于是，得

BD

=(-

7

5

，

1

5

)，

BC

=(1，1)，故向量

BC

和

BD

的夹角∠DBC的余弦值为cos∠DBC=

BC • BD

| BC |•| BD |

=-

3

5

，即∠DBC=π-arccos

3

5

所以，

CD

=(π-arccos

3

5

)•

2

≈3.13．

点评：本题两种方法，方法一灵活运用解三角形的相关公式求出弧所对的圆心角的大小，些方法运算量较小，但方法的设计作辅助线等的思维量较大．方法二建立坐标系，求出了两个半径所在线段对应的向量，方法好想，但转化为坐标后运算量较大．请答题者做完本题后，对比两种方法解题的特点．本题中的数据需用把三角数表示，现在的教材已将把三角函数删除，这是本题设计上的不足之处．