题目内容
若不等式x2-ax+a<0的解集为空集,则实数a的取值范围是( )
| A、0≤a≤4 |
| B、0<a<4 |
| C、a<0或a>4 |
| D、a≤0或a≥4 |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:根据不等式x2-ax+a<0的解集为空集时,△≤0,求出a的取值范围.
解答:
解:∵不等式x2-ax+a<0的解集为空集,
∴△=(-a)2-4a≤0,
即a(a-4)≤0;
解得0≤a≤4,
∴实数a的取值范围是0≤a≤4.
故选:A.
∴△=(-a)2-4a≤0,
即a(a-4)≤0;
解得0≤a≤4,
∴实数a的取值范围是0≤a≤4.
故选:A.
点评:本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
数列{xn}对任意n∈N*满足(1+xn)(1-xn+1)=2,且x1=2,则x2013•x2015的值为( )
| A、2 | B、1 | C、0 | D、-1 |
若函数f(x)=5loga(3x-8)+1(a>0,且a≠1),则f(x)过定点( )
| A、(1,3) |
| B、(1,1) |
| C、(5,1) |
| D、(3,1) |
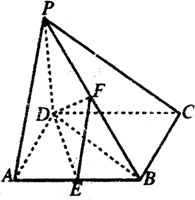 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是PB,AB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是PB,AB的中点.