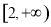题目内容
已知 ABC的三边为a,b,c.其面积S=
ABC的三边为a,b,c.其面积S= 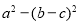 ,且b+c=8.
,且b+c=8.
(1)求cosA
(2)求S的最大值
练习册系列答案
相关题目
5.已知$\overrightarrow{MN}=\overrightarrow a+5\overrightarrow b$,$\overrightarrow{NP}=-2(\overrightarrow a-4\overrightarrow b)$,$\overrightarrow{PQ}=3(\overrightarrow a-\overrightarrow b)$,则( )
| A. | M,N,P三点共线 | B. | M,N,Q三点共线 | C. | M,P,Q三点共线 | D. | N,P,Q三点共线 |
12.某市为鼓励居民节约用水,将实行阶梯水价,该市每户居民每月用水量划分为三级,水价实行分级递增.第一级水量:用水量不超过20吨,水价标准为1.5元/吨; 第二级水量:用水量超过20但不超过30吨,超出第一级水量的部分,水价为2.25元/吨; 第三级水量:用水量超过30吨,超出第二级水量的部分,水价为3.0元/吨.随机调查了该市1000户居民,获得了他们某月的用水量数据,整理得到如下的频率分布表:
(Ⅰ)根据频率分布表中的数据,写出a,b,c的值;从该市调查的1000户居民中随机抽取一户居民,求该户居民用水量不超过30吨的概率;
(Ⅱ)从1000户居民中按用水三个等级分层抽取5户幸运者,发给大奖两份和幸运奖三份共5份,每户一份,求两份大奖获得者的都是节水型用户(用水量不超过20吨的居民)的概率.
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
(Ⅱ)从1000户居民中按用水三个等级分层抽取5户幸运者,发给大奖两份和幸运奖三份共5份,每户一份,求两份大奖获得者的都是节水型用户(用水量不超过20吨的居民)的概率.


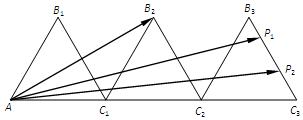 如图,△AB1C1,△C1B2C2,△C2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有2个不同的点P1,P2,则$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=36.
如图,△AB1C1,△C1B2C2,△C2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有2个不同的点P1,P2,则$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=36. ,
, ,则
,则  在
在 上的投影为
上的投影为 B.
B. C.
C. D.
D.
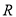 上的函数
上的函数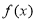 为单调函数,且对任意
为单调函数,且对任意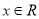 ,恒有
,恒有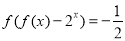 ,若
,若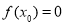 ,则
,则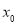 的值是( )
的值是( )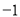 B.
B.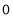 C.
C.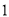 D.
D.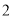
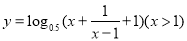 的值域是( )
的值域是( )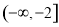 B、
B、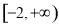 C、
C、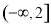 D、
D、