题目内容
已知椭圆
+y2=1的左、右焦点分别为F1，F2，点P在椭圆上，当△F1PF2的面积为1时，
•
=（ ）
| x2 |
| 4 |
| PF1 |
| PF2 |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用椭圆的定义、余弦定理、三角形的面积公式，即可得出结论．
解答：
解：由已知得a=2，设|PF1|=m，|PF2|=n，∠F2PF1=α
由椭圆的定义可知m+n=4，平方可得m2+n2+2mn=4
∵m2+n2-2mncosα=12，
mnsinα=1
∴α=90°，
∴
•
=0．
故选：A．
由椭圆的定义可知m+n=4，平方可得m2+n2+2mn=4
∵m2+n2-2mncosα=12，
| 1 |
| 2 |
∴α=90°，
∴
| PF1 |
| PF2 |
故选：A．
点评：本题考查椭圆的定义、余弦定理、三角形的面积公式，考查学生的计算能力，属于中档题．
练习册系列答案
通城学典默写能手系列答案
相关题目
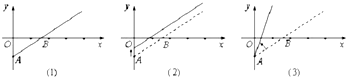如图（1）是反应某公共汽车线路收支差额（即营运所得票价收入与付出成本的差）y与乘客两x之间关系的图象．由于目前该条公交线亏损，公司有关人员提出了两种调整的建议，如图（2）（3）的实线（虚线为原参考线）所示．给出下列说法：cos（-
π）的值是（ ）
| 43 |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知sin（
+α）=
，则cosα的值为（ ）
| 5π |
| 2 |
| 2 |
| 5 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、±
|
命题“?x∈R，x2+x≥2”的否定是（ ）
| A、?x0∈R，x2+x≤2 |
| B、?x0∈R，x2+x＜2 |
| C、?x∈R，x2+x≤2 |
| D、?x∈R，x2+x＜2 |
