题目内容
9.将一个数列中部分项按原来的先后次序排列所成的一个新数列称为原数列的一个子数列.如果数列存在成等比数列的子数列,那么称该数列为“弱等比数列”.已知m>1,设区间(m,+∞)内的三个正整数a,x,y满足:数列a2,$\sqrt{{y}^{2}-1}$,cos$\frac{π}{2}$,x2-1为“弱等比数列”,则$\frac{a}{x}$的最小值为2.分析 由新定义可得数列a2,$\sqrt{{y}^{2}-1}$,x2-1为等比数列,进一步得到$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}-\frac{{y}^{2}}{{a}^{2}-1}=1$,由此可得$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}≤1$,即${x}^{2}≤\frac{{a}^{2}-1}{{a}^{2}}$,再转化为只含a的代数式,配方后利用基本不等式求最值.
解答 解:由题意,数列a2,$\sqrt{{y}^{2}-1}$,cos$\frac{π}{2}$,x2-1为“弱等比数列”,
则数列a2,$\sqrt{{y}^{2}-1}$,x2-1为等比数列,
∴y2-1=a2(x2-1),
即a2x2-y2=a2-1,
由题意可知,a>1,
∴$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}-\frac{{y}^{2}}{{a}^{2}-1}=1$,
则$\frac{{x}^{2}}{\frac{{a}^{2}-1}{{a}^{2}}}≤1$,∴${x}^{2}≤\frac{{a}^{2}-1}{{a}^{2}}$,
则$\frac{{a}^{2}}{{x}^{2}}≥\frac{{a}^{4}}{{a}^{2}-1}$=$\frac{({a}^{2}-1)^{2}+2({a}^{2}-1)+1}{{a}^{2}-1}$=$({a}^{2}-1)+\frac{1}{{a}^{2}-1}+2≥4$,
当且仅当${a}^{2}-1=\frac{1}{{a}^{2}-1}$,即a=2(a>1)时取等号.
∴$\frac{a}{x}≥2$(a>1,x>1).
即$\frac{a}{x}$的最小值为2.
故答案为:2.
点评 本题考查数列递推式,考查了数列的函数特性,训练了利用基本不等式求最值,是难题.

| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
 如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连结BC1,过B1作B1E⊥BC1交CC1于点E.
如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连结BC1,过B1作B1E⊥BC1交CC1于点E.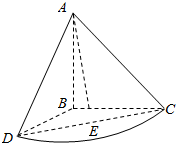 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求: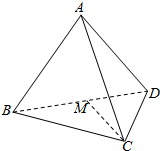 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.