若复数z满足(1-i2)z=1+i3.则z的虚部为( )A．0B．$\frac{1}{2}$C．1D．-$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

1．若复数z满足（1-i²）z=1+i³，则z的虚部为（　　）

A．

B．

$\frac{1}{2}$

C．

D．

-$\frac{1}{2}$

分析把已知的等式变形，利用复数代数形式的乘除运算化简得答案．

解答解：由（1-i²）z=1+i³，
得$z=\frac{1+{i}^{3}}{1-{i}^{2}}=\frac{1-i}{2}=\frac{1}{2}-\frac{i}{2}$，
∴z的虚部为-$\frac{1}{2}$．
故选：D．

点评本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案

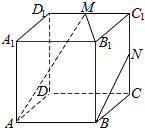
	A．	直线MN与DC₁互相垂直		B．	直线AM与BN互相平行
	C．	直线MN与BC₁所成角为90°		D．	直线MN垂直于平面A₁BCD₁

12．若函数f（x）=x²+ax+$\frac{1}{x}$在[$\frac{1}{3}$，+∞）上是增函数，则实数a的取值范围是（　　）

9．已知抛物线x²=2py（p＞0），斜率为1的直线交抛物线于A，B两点，若线段AB中点的横坐标为2，则该抛物线的准线方程为（　　）

16．已知a，b是两条不重合的直线，α，β是两个不同的平面，则下列命题中正确的是（　　）

	A．	若a⊥b，a⊥α，则b∥α		B．	若a⊥α，b∥α，则a⊥b
	C．	若a∥b，b?α，则a∥α		D．	若a，b?α，a∥β，b∥β，则α∥β

6．已知等比数列{a_n}的公比q＞1，a₁=2，且a₁，a₂，a₃-8成等差数列，数列{a_nb_n}的前n项和为$\frac{（2n-1）•3^n+1}{2}$．
（1）分别求出数列{a_n}和{b_n}的通项公式；
（2）设数列{$\frac{1}{a_n}$}的前n项和为S_n，已知?_n∈N^*，S_n≤m恒成立，求实数m的最小值．

13．若函数f（x）的定义域为D，任取x₁、x₂∈D，都有|f（x₁）-f（x₂）|≤|x₁-x₂|成立，则称f（x）为D上的“收缩”函数．）
（1）判断f（x）=$\frac{1}{4}$x²+$\frac{1}{2}$x在[-1，1]上是否为“收缩”函数，并说明理由；
（2）是否存在k∈R，使f（x）=k$\sqrt{{x}^{2}+1}$在R上位“收缩“函数，若存在，求k的取值范围，若不存在，说明理由；
（3）若D=[0，1]，f（0）=f（1），且f（x）为”收缩“函数，?x₁、x₂∈D，|f（x₁）-f（x₂）|≤$\frac{1}{2}$能否恒成立并说明理由？

10．

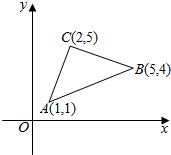如图，已知A（1，1），B（5，4），C（2，5），设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量．
（1）求单位向量$\overrightarrow{a}$的坐标；
（2）求向量$\overrightarrow{AC}$在向量$\overrightarrow{a}$上的投影；
（3）求△ABC的面积S_△ABC．

11．

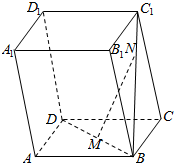如图所示，已知几何体ABCD-A₁B₁C₁D₁是平行六面体．
（1）化简$\frac{1}{2}$$\overrightarrow{A{A}_{1}}$+$\overrightarrow{BC}$+$\frac{2}{3}$$\overrightarrow{AB}$，并在图上标出结果；
（2）设M是底面ABCD的中心，N是侧面BCC₁B₁对角线BC₁上的点，且C₁N=$\frac{1}{4}$C₁B，设$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{A{A}_{1}}$，求α，β，γ的值．

试题分类