题目内容
 圆锥的底面半径为10cm,高为20
圆锥的底面半径为10cm,高为20| 2 |
考点:多面体和旋转体表面上的最短距离问题
专题:空间位置关系与距离
分析:将圆锥侧面展开,进而根据平面上两点之间的距离,线段最短,求出最短路程.
解答:
解:∵圆锥的底面半径为10cm,高为20
cm,
故圆锥的母线长l=
=30cm,
故圆锥侧面展开图的圆心角α满足:
=
,
故α=120°,
如下图所示:
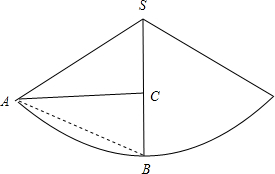
则AC的长度即为所求最短路程,
连接AB,可得△SAB为边长为30cm的等边三角形,
故AC=
×30=15
cm,
故从点A出发在侧面上运动到点C的最短路程为15
cm.
| 2 |
故圆锥的母线长l=
102+(20
|
故圆锥侧面展开图的圆心角α满足:
| α |
| 360° |
| 10 |
| 30 |
故α=120°,
如下图所示:

则AC的长度即为所求最短路程,
连接AB,可得△SAB为边长为30cm的等边三角形,
故AC=
| ||
| 2 |
| 3 |
故从点A出发在侧面上运动到点C的最短路程为15
| 3 |
点评:考查圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
老师在班级50名学生中,依次抽取班号为4,14,24,34,44的学生进行作业检查,老师运用的抽样方法是( )
| A、随机数法 | B、抽签法 |
| C、系统抽样 | D、以上都是 |
已知集合A={x∈R|-3≤x≤4},B={x∈R|log2x≥1},则A∩B=( )
| A、[4,+∞) |
| B、(4,+∞) |
| C、[2,4) |
| D、[2,4] |
设f(x)=
,则f(x)+f(
)等于( )
| x-1 |
| x+1 |
| 1 |
| x |
A、
| ||
B、
| ||
| C、0 | ||
| D、-1 |
已知集合P={x|0≤x≤4},集合N={y|0≤y≤2},下列从P到Q的各对应关系f不是函数的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
 如图,在四边形ABCD中,AB=CD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
如图,在四边形ABCD中,AB=CD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.