题目内容

9．函数f（x）=x2-x-2的零点是2或-1．

分析 由零点的定义，令f（x）=0，由二次方程的解法，运用因式分解解方程即可得到所求函数的零点．

解答 解：令f（x）=0，
即x2-x-2=0，
即有（x-2）（x+1）=0，
解得x=2或x=-1．
即函数f（x）的零点为2或-1．
故答案为：2或-1．

点评 本题考查函数的零点的求法，注意运用方程思想，考查运算能力，属于基础题．

练习册系列答案
相关题目
19．过双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的右焦点F作双曲线的一条渐近线的垂线，垂足为E，O为坐标原点，若∠OFE=2∠EOF，则b=（　　）
A．$\frac{1}{2}$B．$\sqrt{3}$C．2D．$\frac{\sqrt{3}}{3}$
20．某几何体的三视图如图所示，则该几何体的表面积为（　　）
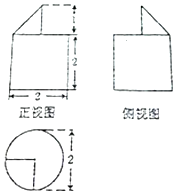
A．6π+1B．$\frac{{（{24+\sqrt{2}}）π}}{4}+1$C．$\frac{{（{23+\sqrt{2}}）π}}{4}+\frac{1}{2}$D．$\frac{{（{23+\sqrt{2}}）π}}{4}+1$
17．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，使得|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|成立的一个充分非必要条件是（　　）
A．$\overrightarrow{a}$∥$\overrightarrow{b}$B．$\overrightarrow{a}$+2$\overrightarrow{b}$=0C．$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$+$\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$=0D．2$\overrightarrow{a}$+$\overrightarrow{b}$=0
4．已知集合M={x|x2-3x=0}，N={x|x＞-1}，则M∩N=（　　）
A．（-1，0）B．（0，3）C．{0，3}D．{3}
14．已知椭圆x2+2y2=m（m＞0），以椭圆内一点M（2，1）为中点作弦AB，设线段AB的中垂线与椭圆相交于C，D两点．
（Ⅰ）求椭圆的离心率；
（Ⅱ）试判断是否存在这样的m，使得A，B，C，D在同一个圆上，并说明理由．
1．在△ABC中，内角A，B，C的对边分别为a，b，c，已知B=60°，b=7，sinA-sinC=$\frac{3\sqrt{3}}{14}$．
（Ⅰ）求a；
（Ⅱ）求cos（2A-B）的值．
18．在平面直角坐标系xOy中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C的极坐标方程ρ=2$\sqrt{2}$sin（θ+$\frac{π}{4}$）．倾斜角为$\frac{π}{3}$，且经过定点P（0，1）的直线l与曲线C交于M，N两点
（Ⅰ）写出直线l的参数方程的标准形式，并求曲线C的直角坐标方程；
（Ⅱ）求$\frac{1}{|PM|}$+$\frac{1}{|PN|}$的值．
19．已知抛物线y2=4x的焦点为F，过焦点F的直线交抛物线于A、B两点，O为坐标原点，若|AB|=6，则△AOB的面积为（　　）
A．$\sqrt{6}$B．$2\sqrt{2}$C．$2\sqrt{3}$D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网