题目内容
19.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,且离心率为$\frac{\sqrt{3}}{3}$,M为椭圆上一点,△MF1F2的周长为2$\sqrt{3}$+2.(1)求椭圆E的方程;
(2)若直线l过点F2,l与圆O:x2+y2=5相交于P,Q两点,l与椭圆E相交于R,S两点,若|PQ|∈[4,$\sqrt{19}$],求△F1RS的面积的最大值和最小值.
分析 (1)由已知得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,2a+2c=2$\sqrt{3}$+2,由此能求出椭圆的方程.
(2)设l:x=my+1,与椭圆联立,得(2m2+3)y2+4my-4=0,由此利用点到直线距离公式、根的判别式、韦达定理、弦长公式,结合题意条件能求出△F1RS的面积的最大值和最小值.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{3}$,∴e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,①
∵F1,F2是椭圆C的两个焦点,P是C上任意一点,且△PF1F2的周长为2$\sqrt{3}$+2,
∴2a+2c=2$\sqrt{3}+2$,②
联立①②,解得a=$\sqrt{3}$,c=1,∴b2=3-1=2,
∴椭圆的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1.
(2)由题知直线l的斜率为0时不满足题意,
设l:x=my+1,O到l的距离d=$\frac{1}{\sqrt{1+{m}^{2}}}$,
∴|PQ|=2$\sqrt{5-\frac{1}{1+{m}^{2}}}$∈[4,$\sqrt{19}$],∴0≤m2≤3.
联立$\left\{\begin{array}{l}{x=my+1}\\{2{x}^{2}+3{y}^{2}=6}\end{array}\right.$,得(2m2+3)y2+4my-4=0,
△=(4m)2+16(2m2+3)>0恒成立,
设R(x1,y1),S(x2,y2),则${y}_{1}+{y}_{2}=\frac{-4m}{2{m}^{2}+3}$,${y}_{1}{y}_{2}=\frac{-4}{2{m}^{2}+3}$,
∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{\frac{16{m}^{2}}{(2{m}^{2}+3)^{2}}+\frac{16}{2{m}^{2}+3}}$=$\frac{4\sqrt{3({m}^{2}+1)}}{2{m}^{2}+3}$,
∴${S}_{△{F}_{1}RS}$=$\frac{1}{2}$|y1-y2|•|F1F2|=$\frac{4\sqrt{3({m}^{2}+1)}}{2{m}^{2}+3}$,
令t=m2+1∈[1,4],
∴${S}_{△{F}_{1}RS}=4\sqrt{\frac{3t}{(2t+1)^{2}}}$=$\frac{4\sqrt{3}}{\sqrt{4+(4t+\frac{1}{t})}}$,
∵f(t)=4t+$\frac{1}{t}$在[1,4]上单调递增,∴f(t)=[5,$\frac{65}{4}$],
∴${S}_{△{F}_{1}RS}$∈[$\frac{8\sqrt{3}}{9},\frac{4\sqrt{3}}{3}$],
∴△F1RS的面积的最大值是$\frac{4\sqrt{3}}{3}$,最小值是$\frac{8\sqrt{3}}{9}$.
点评 本题考查椭圆方程的求法,考查三角形面积的最大值及最小值的求法,是中档题,解题时要认真审题,注意点到直线距离公式、根的判别式、韦达定理、弦长公式的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 2-i | B. | -2-i | C. | 2+i | D. | -2+i |
| A. | y=sin$\frac{1}{2}x$,x∈R | B. | y=sin2x,x∈R | C. | y=$\frac{1}{2}$sinx,x∈R | D. | y=2sinx,x∈R |
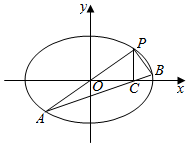 如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.
如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.