题目内容
若曲线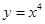 的一条切线l与直线
的一条切线l与直线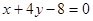 垂直,则l的方程为 ( )
垂直,则l的方程为 ( )
A.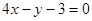 | B.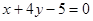 |
C.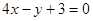 | D.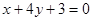 |
A
解析试题分析:设切点为 ,因为切线
,因为切线 与直线
与直线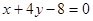 垂直,故其斜率为4,又
垂直,故其斜率为4,又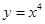 的导数为
的导数为 ,所以
,所以 ,所以
,所以 ,所以
,所以 ,所以
,所以 的方程为
的方程为 .
.
考点:导数的几何意义 两直线相互垂直的判定
点评:本题主要考查了导数的几何意义,考查两条直线垂直,直线的斜率的关系,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
设函数y=f(x),x∈R的导函数为 ,且
,且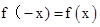 ,
, ,则下列成立的是( )
,则下列成立的是( )
| A.f(0)<e?1f(1)<e2f(2) | B.e2f(2)< f(0)<e?1f(1) |
| C.e2f(2)<e?1f(1)<f(0) | D.e?1f(1)<f(0)<e2f(2) |
函数f(x)=(x-3)ex的单调递增区间是( )
| A.(-∞,2) | B.(0,3) | C.(1,4) | D.(2,+∞) |
设 是可导函数,且
是可导函数,且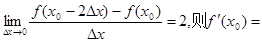 ( )
( )
A.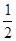 | B.-1 | C.0 | D.-2 |
函数
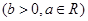 在点
在点 处的切线斜率的最小值是( )
处的切线斜率的最小值是( )
A. | B. | C. | D. |
已知函数 的图象如图,则
的图象如图,则 与
与 的大小关系是( )
的大小关系是( ) 
A. > > |
B. < < |
C. = = |
| D.不能确定 |
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
| A.1个 | B.2个 |
| C.3个 | D.4个 |
 ,那么,原油温度的瞬时变化率的最小值是( )
,那么,原油温度的瞬时变化率的最小值是( )


 是函数
是函数 的导函数,如果
的导函数,如果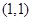 ,那么曲线
,那么曲线 的取值范围是
的取值范围是