题目内容
函数
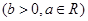 在点
在点 处的切线斜率的最小值是( )
处的切线斜率的最小值是( )
A. | B. | C. | D. |
A
解析试题分析:根据题意,由于函数
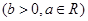 在点
在点 处的切线斜率
处的切线斜率 ,当且仅当b=
,当且仅当b=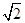 时取得等号,故答案为A.
时取得等号,故答案为A.
考点:由导数求出切线的斜率
点评:此题是一道综合题,要求学生会根据导数求出切线的斜率,掌握不等式恒成立时所取的条件,利用会利用基本不等式求函数的最小值及会求二次函数的最小值.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
设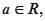 函数
函数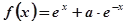 的导函数是
的导函数是 且
且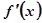 是奇函数,若曲线
是奇函数,若曲线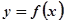 的一条切线的斜率是
的一条切线的斜率是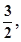 则切点的横坐标为( )
则切点的横坐标为( )
A. | B.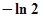 | C.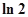 | D. |
已知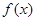 是定义在
是定义在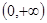 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若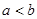 ,则
,则 的大小关系为
的大小关系为
A. | B.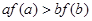 |
C.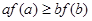 | D. |
若曲线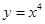 的一条切线l与直线
的一条切线l与直线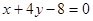 垂直,则l的方程为 ( )
垂直,则l的方程为 ( )
A.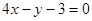 | B.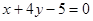 |
C.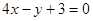 | D.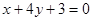 |
曲线 在P点处的切线平行于直线
在P点处的切线平行于直线 ,则此切线方程是( )
,则此切线方程是( )
A. | B. |
C. | D. |
已知函数 的导函数为
的导函数为 ,
,
 1,1),且
1,1),且 ,如果
,如果 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A.( ) ) | B.  | C. | D. |
已知 在R上可导,且
在R上可导,且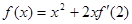 ,则
,则 的大小关系是( )
的大小关系是( )
A.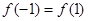 | B. |
C. | D.不确定 |
设 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集是 ( )
的解集是 ( )
A. | B. |
C. | D. |
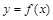 的图象如图所示,则导函数
的图象如图所示,则导函数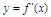 的图象可能是 ( )
的图象可能是 ( ) 