题目内容
2.函数f(x)=sinx+cos(x+$\frac{π}{6}$)的最小值和最小正周期分别是( )| A. | -$\sqrt{3}$,π | B. | -1,π | C. | -$\sqrt{3}$,2π | D. | -1,2π |
分析 化简函数f(x),从而求出函数的最小值和最小正周期.
解答 解:函数f(x)=sinx+cos(x+$\frac{π}{6}$)=sinx+$\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx=sin(x+$\frac{π}{3}$),
故函数的最小正周期等于$\frac{2π}{1}$=2π,
当x=2kπ-$\frac{π}{2}$,k∈z时,函数有最小值等于-1.
故选:D.
点评 本题考查了三角函数问题,考查求最小值和最小正周期,熟练掌握三角函数的性质是解题的关键,是一道基础题.

练习册系列答案
相关题目
13.对于平面α,直线m,n给出下列命题
①若m∥n,则m,n与α所成的角相等.
②若m∥n,n∥α,则m∥α.
③若m⊥α,m⊥n,则n⊥α
④若m与n异面且m∥α,则n与α相交,
其中正确命题个数有( )个.
①若m∥n,则m,n与α所成的角相等.
②若m∥n,n∥α,则m∥α.
③若m⊥α,m⊥n,则n⊥α
④若m与n异面且m∥α,则n与α相交,
其中正确命题个数有( )个.
| A. | 4 | B. | 2 | C. | 3 | D. | 1 |
10.下列角中与-200°角终边相同角( )
| A. | 200° | B. | -160° | C. | 160° | D. | 20° |
17.马云同学向某银行贷款M万元,用于购买某件商品,贷款的月利率为5%(按复利计算),按照还款合同,马云同学每个月都还款x万元,20个月还清,则下列关系式正确的是( )
| A. | 20x=M | B. | 20x=M(1+5%)20 | C. | 20x<M(1+5%)20 | D. | 20x>M(1+5%)20 |
14.设f(x)=lnx+$\frac{1}{x}$,则f(sin$\frac{π}{5}$)与f(cos$\frac{π}{5}$)的大小关系是( )
| A. | f(sin$\frac{π}{5}$)>f(cos$\frac{π}{5}$) | B. | f(sin$\frac{π}{5}$)<f(cos$\frac{π}{5}$) | C. | f(sin$\frac{π}{5}$)=f(cos$\frac{π}{5}$) | D. | 大小不确定 |
12.已知各项均为正数的等比数列{an}满足a3•a5=64,a2=2,则a1=( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
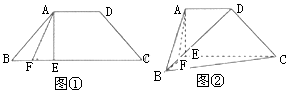 如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.
如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.