题目内容
在电视台举行的“十八大知识竞赛”中,答对一题得1分,弃权得0分,答错扣1分,甲队答其中一题的得分X的分布列如
下:
若E(X)=
,则D(X)的值是 .
下:
| X | -1 | 0 | 1 | ||
| P | a |
| c |
| 1 |
| 3 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由离散型随机变量的分布列的性质和数学期望计算公式,列出方程组,求出a,b,由此能求出D(X)的值.
解答:
解:由已知得
,
解得a=
,c=
,
∴D(X)=(-1-
)2×
+(0-
)2×
+(1-
)2×
=
.
故答案为:
.
|
解得a=
| 1 |
| 6 |
| 1 |
| 2 |
∴D(X)=(-1-
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:本题考查离散型随机变量的方差的值的求法,是基础题,解题时要认真审题,注意离散型随机变量的分布列的性质和数学期望、方差计算公式的合理运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
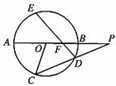 如图,⊙O的直径AB=4,弦CD所在直线与AB的延长线交于点P,且
如图,⊙O的直径AB=4,弦CD所在直线与AB的延长线交于点P,且
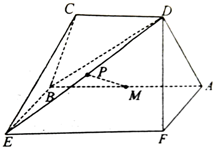 如图等腰梯形ABCD中,AB∥CD,AD⊥BD,M为AB的中点,矩形ABEF所在的平面和平面ABCD相互垂直.
如图等腰梯形ABCD中,AB∥CD,AD⊥BD,M为AB的中点,矩形ABEF所在的平面和平面ABCD相互垂直.