题目内容
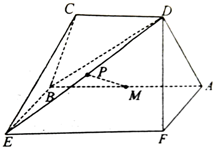 如图等腰梯形ABCD中,AB∥CD,AD⊥BD,M为AB的中点,矩形ABEF所在的平面和平面ABCD相互垂直.
如图等腰梯形ABCD中,AB∥CD,AD⊥BD,M为AB的中点,矩形ABEF所在的平面和平面ABCD相互垂直.(1)求证:AD⊥平面DBE
(2)设DE的中点为P,求证MP∥平面DAF
(3)若AB=2,AD=AF=1求三棱锥E-BCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)要证线与面垂直,需先证明直线AF垂直于平面内的两条相交直线,因为矩形ABCD所在的平面和平面ABEF互相垂直,所以BC垂直于平面ABEF,从而AF垂直于BC,依题意,AF垂直于BF,从而命题得证.
(2)取DF的中点为N,由三角形中位线定理,MN平行CD且等于CD的一半,而OA也是如此,从而MN平行且等于OA,四边形MNAO为平行四边形,所以OM平行于AN,由线面平行的判定定理即可得证OM平行于平面DAF.
(3)先计算底面三角形BEF的面积,在等腰梯形ABEF中,可得此三角形的高为
,底EF为1,再计算三棱锥C-BEF的高,即为CB,最后由三棱锥体积计算公式计算即可.
(2)取DF的中点为N,由三角形中位线定理,MN平行CD且等于CD的一半,而OA也是如此,从而MN平行且等于OA,四边形MNAO为平行四边形,所以OM平行于AN,由线面平行的判定定理即可得证OM平行于平面DAF.
(3)先计算底面三角形BEF的面积,在等腰梯形ABEF中,可得此三角形的高为
| ||
| 2 |
解答:
证明:(1)∵面ABCD⊥面ABEF,
面ABCD∩面ABEF=AB,
∵矩形ABEF,
∴EB⊥AB,
∵EB?面ABEF,
∴EB⊥面ABCD,
∵AD?面ABCD,
∴EB⊥AD,AD⊥BD,BD∩BE=B,
∴AD⊥面BDE.
(2)取DF的中点N,连接PN,AN,
因为P为DE 的中点,
∴PN∥EF,PN=
EF,
∵M为AB的中点
∴AM∥EF,AM=
EF,即AM∥PN,AM=PN,
即四边形AMPN为平行四边形,
∴AN∥PM,
∵PM?面ADF,AN?面ADF,
所以MP∥平面DAF.
(3)∵AF=1,AD⊥BD,AB=2,
∴∠DAB=60°
过点C作CH⊥AB于H,则∠CBH=60°,
∴CH=
,CF=AB-2HB=1,
故S△BCF=
×1×
=
.
∵EB⊥平面ABCD,
∴三棱锥E-BCD的高为EB=1,
∴VE-BCD=
×S△BCD×BE=
×
×1=
.
面ABCD∩面ABEF=AB,
∵矩形ABEF,
∴EB⊥AB,
∵EB?面ABEF,
∴EB⊥面ABCD,
∵AD?面ABCD,
∴EB⊥AD,AD⊥BD,BD∩BE=B,
∴AD⊥面BDE.

(2)取DF的中点N,连接PN,AN,
因为P为DE 的中点,
∴PN∥EF,PN=
| 1 |
| 2 |
∵M为AB的中点
∴AM∥EF,AM=
| 1 |
| 2 |
即四边形AMPN为平行四边形,
∴AN∥PM,
∵PM?面ADF,AN?面ADF,
所以MP∥平面DAF.
(3)∵AF=1,AD⊥BD,AB=2,
∴∠DAB=60°
过点C作CH⊥AB于H,则∠CBH=60°,
∴CH=
| ||
| 2 |
故S△BCF=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∵EB⊥平面ABCD,
∴三棱锥E-BCD的高为EB=1,
∴VE-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
点评:本题考查了线面垂直的判定定理和性质定理的运用,线面平行的判定定理和性质定理的运用,椎体体积计算公式及其计算方法,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目