题目内容
设椭圆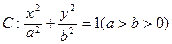 的一个顶点与抛物线
的一个顶点与抛物线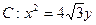 的焦点重合,
的焦点重合,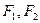 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率 且过椭圆右焦点
且过椭圆右焦点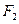 的直线
的直线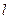 与椭圆C交于
与椭圆C交于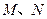 两点.
两点.
(1)求椭圆C的方程;
(2)是否存在直线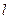 ,使得
,使得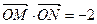 .若存在,求出直线
.若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(3)若AB是椭圆C经过原点O的弦, MN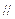 AB,求证:
AB,求证: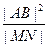 为定值
为定值
解:椭圆的顶点为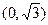 ,即
,即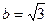
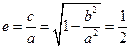 ,解得
,解得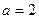 ,
, 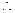 椭圆的标准方程为
椭圆的标准方程为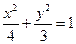 …… 3分
…… 3分
(2)由题可知,直线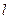 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意.
②设存在直线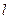 为
为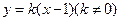 ,且
,且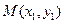 ,
, .
.
由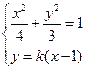 得
得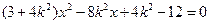 ,
, 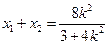 ,
,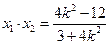 ,
,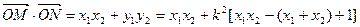
=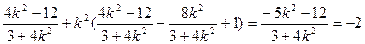
所以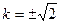 ,故直线
,故直线 的方程为
的方程为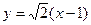 或
或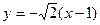 …………8分
…………8分
(3)设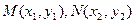 ,
,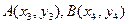
由(2)可得: |MN|=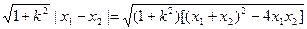
=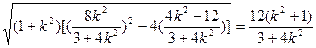 .
.
由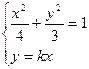 消去y,并整理得:
消去y,并整理得: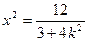 ,
,
|AB|=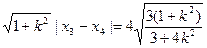 ,∴
,∴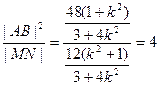 为定值
为定值
解析

练习册系列答案
相关题目
极坐标系中,由三条曲线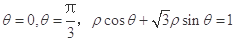 围成的图形的面积是( )
围成的图形的面积是( )
A.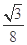 | B.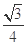 | C.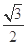 | D. |
 ,
,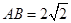 ,
,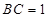 ,以
,以 的中点
的中点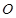 为
为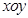 .
.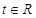 ,探究
,探究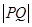 的最
的最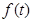 。
。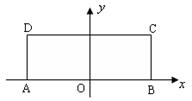
 ?若存在,求出m的取值范围,若不存在,请说明理由.
?若存在,求出m的取值范围,若不存在,请说明理由.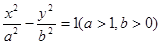 的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为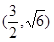 ,求抛物线的方程和双曲线的方程。
,求抛物线的方程和双曲线的方程。 与抛物线
与抛物线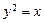 交于
交于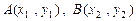 两点,与
两点,与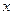 轴相交于点
轴相交于点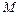 ,且
,且 .
.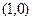 ;
;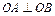 ;
;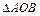 的面积的最小值.
的面积的最小值.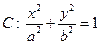 (
(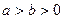 )的一个焦点坐标为
)的一个焦点坐标为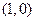 ,且长轴长是短轴长的
,且长轴长是短轴长的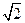 倍.
倍.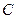 的方程;
的方程; 为坐标原点,椭圆
为坐标原点,椭圆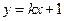 相交于两个不同的点
相交于两个不同的点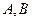 ,线段
,线段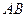 的中点为
的中点为 ,若直线
,若直线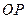 的斜率为
的斜率为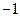 ,求△
,求△ 的面积.
的面积.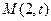
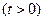 在直线
在直线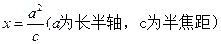 上。
上。 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;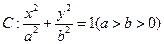 的离心率
的离心率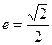 ,过右焦点
,过右焦点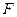
 的直线
的直线 与椭圆
与椭圆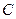 相交
相交 到直线
到直线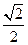
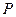 ,使得当直线
,使得当直线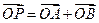 成
成