题目内容
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1
(1)求曲线C的方程.
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有 ?若存在,求出m的取值范围,若不存在,请说明理由.
?若存在,求出m的取值范围,若不存在,请说明理由.
解:(Ⅰ)设P(x,y)是曲线C上任意一点,那么点P(x,y)满足:
化简得 .
.
(Ⅱ)设过点M(m,0)(m>0)的直线l与曲线C的交点为A ,B
,B 。
。
设l的方程为x=ty+m,由 得
得 ,△=16(
,△=16( +m)>0,
+m)>0,
于是 ①
①
又 。
。
 =
= +1+
+1+ <0②
<0②
又 ,于是不等式②等价于
,于是不等式②等价于
 ③
③
由①式,不等式③等价于 ④
④
对任意实数t, 的最小值为0,所以不等式④对于一切t成立等价于
的最小值为0,所以不等式④对于一切t成立等价于 ,即
,即 。
。
由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有 ,且m的取值范围
,且m的取值范围 。
。
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
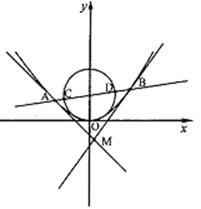
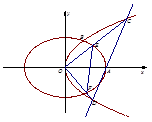
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆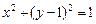 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明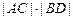 为定值;
为定值;
|
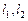 且
且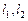 交于点M,求
交于点M,求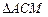 与
与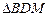 面积之和的最小值.
面积之和的最小值. 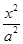 +
+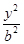 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,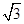 ,
,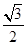 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.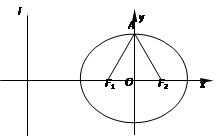
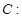
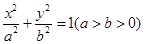 的离心率为
的离心率为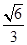 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为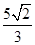 .
.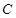 的方程;
的方程;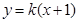 与椭圆
与椭圆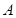 、
、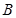 两点.
两点.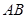 中点的横坐标为
中点的横坐标为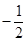 ,求斜率
,求斜率 的值;
的值;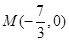 ,求证:
,求证: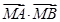 为定值.
为定值.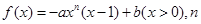 为正整数,
为正整数,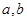 为常数.曲线
为常数.曲线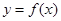 在点
在点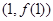 处的切线方程为
处的切线方程为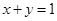 .
.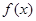 的最大值;
的最大值;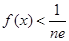 .
.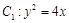 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆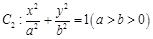 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为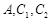 在第一象限的交点为
在第一象限的交点为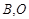 为坐标原点,且
为坐标原点,且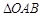 的面积为
的面积为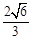
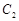 的标准方程;
的标准方程;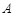 作直线
作直线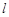 交
交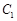 于
于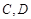 两点,射线
两点,射线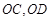 分别交
分别交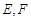 两点.
两点.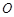 点在以
点在以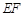 为直径的圆的内部;
为直径的圆的内部;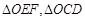 的面积分别为
的面积分别为 ,问是否存在直线
,问是否存在直线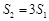 ?请说明理由.
?请说明理由.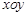 ,
,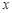 轴在地平面上,
轴在地平面上,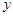 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程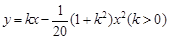 表示的曲线上,其中
表示的曲线上,其中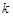 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.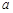 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.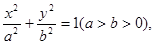 它的一个焦点与抛物线
它的一个焦点与抛物线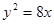 的焦点重合,离心率
的焦点重合,离心率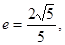 过椭圆的右焦点F作与坐标轴不垂直的直线
过椭圆的右焦点F作与坐标轴不垂直的直线 交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;
交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;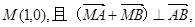 求直线
求直线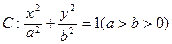 的一个顶点与抛物线
的一个顶点与抛物线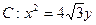 的焦点重合,
的焦点重合,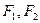 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率 且过椭圆右焦点
且过椭圆右焦点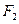 的直线
的直线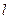 与椭圆C交于
与椭圆C交于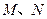 两点.
两点.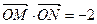 .若存在,求出直线
.若存在,求出直线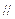 AB,求证:
AB,求证: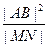 为定值
为定值