题目内容
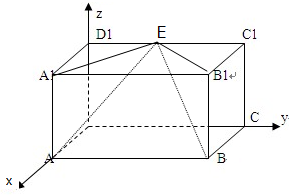
如图,在空间直角坐标系中有长方体ABCD-A1B1C1D1,AB=
,BC=
,AA1=1,E是C1D1的中点,求证:平面AA1E⊥平面BB1E.
| 2 |
| ||
| 2 |

考点:平面与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:建立如图所示的空间直角坐标系,利用向量法能证明A1E⊥平面BB1E,即可证明平面AA1E⊥平面BB1E.
解答:
 证明:建立如图所示的空间直角坐标系,
证明:建立如图所示的空间直角坐标系,
则A(
,0,0),E(0,
,1),B(
,
,0),A1(
,0,1),B1(
,
,1)
∴
=(-
,
-
,1),
=(-
,
,0),
=(-
,
-
,0)
∵
•
=0,
•
=0,
∴A1E⊥BE,A1E⊥B1E,
∴A1E⊥平面BB1E
∵A1E?平面AA1E
∴平面AA1E⊥平面BB1E
 证明:建立如图所示的空间直角坐标系,
证明:建立如图所示的空间直角坐标系,则A(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
∴
| BE |
| ||
| 2 |
| ||
| 2 |
| 2 |
| A1E |
| ||
| 2 |
| ||
| 2 |
| B1E |
| ||
| 2 |
| ||
| 2 |
| 2 |
∵
| A1E |
| BE |
| A1E |
| B1E |
∴A1E⊥BE,A1E⊥B1E,
∴A1E⊥平面BB1E
∵A1E?平面AA1E
∴平面AA1E⊥平面BB1E
点评:本题考查直线与平面垂直的证明,平面与平面垂直的判定,解题时要认真审题,注意向量法的合理运用,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
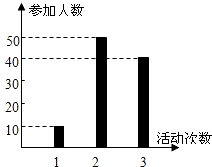 某校高一学生积极参加社会公益活动,成立了公益社,公益社共100人,据统计,他们在今年三月参加公益活动的次数统计如图所示,
某校高一学生积极参加社会公益活动,成立了公益社,公益社共100人,据统计,他们在今年三月参加公益活动的次数统计如图所示,