题目内容
如图①,直线l交x轴、y轴分别于A、B两点,A(a,0)B(0,b),且(a-b)2+|b-4|=0
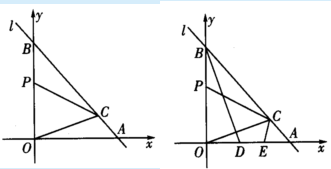
(1)求A、B两点坐标.
(2)C为线段AB上一点,C点的横坐标是3,P是y轴正半轴上一点,且满足∠OCP=45°,求P点坐标.
(3)在(2)的条件下,过B作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.

(1)求A、B两点坐标.
(2)C为线段AB上一点,C点的横坐标是3,P是y轴正半轴上一点,且满足∠OCP=45°,求P点坐标.
(3)在(2)的条件下,过B作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
考点:直线的一般式方程
专题:直线与圆
分析:(1)根据(a-b)2+|b-4|=0,即可求出a=b=4,即可求A、B两点坐标.
(2)求出C的坐标,根据余弦定理即可,求P点坐标.
(3)根据三角形的全等关系证明三角形BFO与三角形BFC全等,即可.
(2)求出C的坐标,根据余弦定理即可,求P点坐标.
(3)根据三角形的全等关系证明三角形BFO与三角形BFC全等,即可.
解答:
解:(1)∵(a-b)2+|b-4|=0,
∴a-b=0且b-4=0,即a=b=4,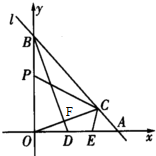
则A(4,0),B(0,4).
(2)直线AB的方程为
+
=1,即x+y=4,
当x=3时,y=1,即C(3,1).
∵P是y轴正半轴上一点,
∴P(0,m),m>0,
则OC=
,CP=
,OP=m,
由余弦定理得cos45°=
=
=
,
平方整理得2m2+5m-25=0,
解得m=-5(舍)或m=
,即P(0,
)
(3)OD=AE;理由如下:连接DC
∵BD垂直于OC
∴∠BFO=∠BFC
又∵C点的纵坐标为3,∠CAD=45°
∴CA=3
,BC=﹙4
﹚2-﹙3
﹚2=4=BO
∴三角形BFO与三角形BFC全等,
∴BD是OC的垂直平分线
∴OD=FC
同理可证明OD=DC=3
,
∵∠CEA=∠BDO,
∴∠ECA=∠CEA
∴EA=CA=OD=3
,
∴OD=AE
∴a-b=0且b-4=0,即a=b=4,

则A(4,0),B(0,4).
(2)直线AB的方程为
| x |
| 4 |
| y |
| 4 |
当x=3时,y=1,即C(3,1).
∵P是y轴正半轴上一点,
∴P(0,m),m>0,
则OC=
| 10 |
| 9+(m-1)2 |
由余弦定理得cos45°=
| OC2+CP2-OP2 |
| 2OC•CP |
| 10+9+(m-1)2-m2 | ||||
2×
|
| ||
| 2 |
平方整理得2m2+5m-25=0,
解得m=-5(舍)或m=
| 5 |
| 2 |
| 5 |
| 2 |
(3)OD=AE;理由如下:连接DC
∵BD垂直于OC
∴∠BFO=∠BFC
又∵C点的纵坐标为3,∠CAD=45°
∴CA=3
| 2 |
| 2 |
| 2 |
∴三角形BFO与三角形BFC全等,
∴BD是OC的垂直平分线
∴OD=FC
同理可证明OD=DC=3
| 2 |
∵∠CEA=∠BDO,
∴∠ECA=∠CEA
∴EA=CA=OD=3
| 2 |
∴OD=AE
点评:本题主要考查直线方程的求解以及三角形全等的应用,综合考查直线的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如表是函数u,v随自变量x变化的一组数据,由此判断u,v最符合的函数模型分别是( )
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| U | 0.0631 | 0.26 | 1.11 | 3.96 | 16.05 | 63.98 |
| v | 11.92 | 14.95 | 18.01 | 21.03 | 24.11 | 26.95 |
| A、二次函数型和一次函数型 |
| B、指数函数型和一次函数型 |
| C、二次函数型和对数函数型 |
| D、指数函数型和对数函数型 |