题目内容
函数y=log2(x2-3x-4)的单调增区间是 .
考点:复合函数的单调性
专题:函数的性质及应用
分析:令t=x2-3x-4>0,求得函数的定义域,根据y=log2t,本题即求二次函数t的增区间,再利用二次函数的性质可得函数t的增区间.
解答:
解:令t=x2-3x-4>0,求得x<-1,或x>4,故函数的定义域为(-∞,-1)∪(4,+∞),
且y=log2t,
故本题即求二次函数t的增区间.
再利用二次函数的性质可得函数t的增区间为(4,+∞),
故答案为:(4,+∞).
且y=log2t,
故本题即求二次函数t的增区间.
再利用二次函数的性质可得函数t的增区间为(4,+∞),
故答案为:(4,+∞).
点评:本题主要考查复合函数的单调性,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于三段论“因为指数函数y=ax是增函数,y=(
)x是指数函数,所以y=(
)x是增函数”,下列说法正确的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、是一个正确的推理 |
| B、大前提错误导致结论错误 |
| C、小前提错误导致结论错误 |
| D、推理形式错误导致结论错误 |
已知α=
,则点P(sinα,tanα)所在的象限是( )
| 5π |
| 8 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(1101)2表示二进制数,将它转换成为十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数(
)2,转换成十进制形式是( )
| ||
| 2002 |
| A、22002-2 |
| B、22002-1 |
| C、22001-2 |
| D、22001-1 |
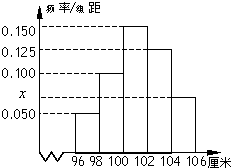 某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].