题目内容
13.设函数f(x)在R上的导函数为f′(x),对?x∈R有f(x)+f(-x)=x2,在(0,+∞)上f′(x)-x<0,若f(4-m)-f(m)≥8-4m,则实数m的取值范围是( )| A. | [2,+∞) | B. | (-∞,2] | C. | (-∞,2]∪[2,+∞) | D. | [-2,2] |
分析 由题意设g(x)=f(x)-$\frac{1}{2}{x}^{2}$,由条件和奇函数的定义判断出g(x)是R上的奇函数,求出g′(x)后结合条件判断出符号,由导数与单调性的关系判断出在(0,+∞)上的单调性,由奇函数的性质判断出在R上的单调性,由g(x)的解析式化简已知的不等式,利用g(x)的单调性列出不等式,求出实数m的取值范围.
解答 解:由题意设g(x)=f(x)-$\frac{1}{2}{x}^{2}$,
∵对?x∈R有f(x)+f(-x)=x2,
∴g(x)+g(-x)=f(x)+f(-x)-x2=0,
则函数g(x)是R上的奇函数,
∵在(0,+∞)上f′(x)-x<0,
∴g′(x)=f′(x)-x<0,则函数g(x)在(0,+∞)上递减,
由奇函数的性质知:函数g(x)在(-∞,+∞)上递减,
∵f(4-m)-f(m)=[g(4-m)+$\frac{1}{2}(4-m)^{2}$]-[g(m)+$\frac{1}{2}{m}^{2}$]
=g(4-m)-g(m)+8-4m≥8-4m,
∴g(4-m)≥g(m),则4-m≤m,解得m≥2,
即实数m的取值范围是[2,+∞),
故选A.
点评 本题考查导数与单调性的关系,奇函数的定义以及性质,以及函数单调性的应用,考查转化思想,构造法,化简、变形能力.

练习册系列答案
相关题目
4.设抛物线C:y2=3x的焦点为F,点A为C上一点,若|FA|=3,则直线FA的倾斜角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
5.已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0,2$\sqrt{2}$)(x0>$\frac{p}{2}$)是抛物线C上一点,圆M与线段MF相交于点A,且被直线x=$\frac{p}{2}$截得的弦长为$\sqrt{3}$|MA|,若$\frac{|MA|}{|AF|}$=2,则|AF|等于( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
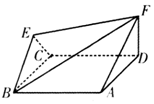 如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.