题目内容
已知|a|＝4，|b|＝8，a与b的夹角是120°.
(1)计算：①|a＋b|，②|4a－2b|；
(2)当k为何值时，(a＋2b)⊥(ka－b)?
解：由已知得，a·b＝4×8×
＝－16.
(1)①∵|a＋b|2＝a2＋2a·b＋b2＝16＋2×(－16)＋64＝48，∴|a＋b|＝4
.
②∵|4a－2b|2＝16a2－16a·b＋4b2＝16×16－16×(－16)＋4×64＝768，
∴|4a－2b|＝16.
(2)∵(a＋2b)⊥(ka－b)，
∴(a＋2b)·(ka－b)＝0，
∴ka2＋(2k－1)a·b－2b2＝0，
即16k－16(2k－1)－2×64＝0.∴k＝－7.
即k＝－7时，a＋2b与ka－b垂直．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
)2＋ln 
－lg 1.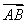
＝e1－e2，
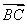＝3e1＋2e2，
＝－8e1－2e2，
，AC＝3，取点D使
＝2
，那么
·
＝( )
等于( )
B．－
若a3＝1，则a1的所有可能取值为________．