题目内容
17.某校高一、高二和高三年级分别有学生1000名、800名和700名,现用分层抽样的方法从中抽取容量为100的样本,则抽出的高二年级的学生人数为32.分析 先求出每个个体被抽到的概率,用高三年级的人数乘以每个个体被抽到的概率,即得高三年级应抽取人数.
解答 解:每个个体被抽到的概率等于 $\frac{100}{700+800+1000}$=$\frac{1}{25}$,
由于高二年级有1000人,故高三年级应抽取的人数为 800×$\frac{1}{25}$=32,
故答案为 32.
点评 本题主要考查分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,属于基础题

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
7.阅读如图的算法框图,输出的结果S的值为( )
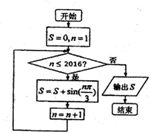

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 0 | D. | -$\frac{\sqrt{3}}{2}$ |
9.在数列{an}中,a1=-1,an+1=an-3,则a4=( )
| A. | -10 | B. | -7 | C. | -5 | D. | 11 |