题目内容
5.等比数列{an}的首项为1,公比为q(q≠1),前n项和为Sn,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$等于( )| A. | $\frac{1}{{S}_{n}}$ | B. | $\frac{{S}_{n}}{{q}^{n-1}}$ | C. | Sn | D. | $\frac{1}{{q}^{n-1}{S}_{n}}$ |
分析 易得数列{$\frac{1}{{a}_{n}}$}是首项为1,公比为$\frac{1}{q}$(q≠1)的等比数列,由求和公式可得.
解答 解:等比数列{an}的首项为1,公比为q(q≠1),前n项和为Sn,
∴数列{$\frac{1}{{a}_{n}}$}是首项为1,公比为$\frac{1}{q}$(q≠1)的等比数列,
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$=$\frac{1×(1-\frac{1}{{q}^{n}})}{1-\frac{1}{q}}$=$\frac{{q}^{n}-1}{{q}^{n-1}(q-1)}$=$\frac{{S}_{n}}{{q}^{n-1}}$,
故选:B.
点评 本题考查等比数列的求和公式,涉及等比数列的判定,属基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
15.记集合M={(x,y)|(x-2cosθ)2+(y-2sinθ)2<1},任取点P∈M,则点P∈{(x,y)|x2+y2≤4}的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{3}$ |
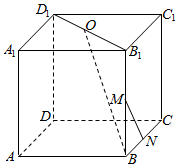 如图,正方体ABCD-A1B1C1D1中,M、N、O分别为BB1,BC,B1D1的中点,求异面直线OB与MN所成角的余弦值.
如图,正方体ABCD-A1B1C1D1中,M、N、O分别为BB1,BC,B1D1的中点,求异面直线OB与MN所成角的余弦值.