题目内容
已知函数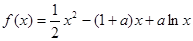 ,其中
,其中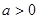 .
.
(Ⅰ) 求函数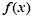 的极小值点;
的极小值点;
(Ⅱ)若曲线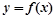 在点
在点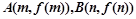 处的切线都与
处的切线都与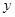 轴垂直,问是否存在常数
轴垂直,问是否存在常数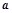 ,使函数
,使函数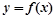 在区间
在区间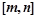 上存在零点?如果存在,求
上存在零点?如果存在,求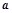 的值:如果不存在,请说明理由.
的值:如果不存在,请说明理由.
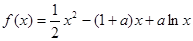 ,其中
,其中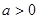 .
.(Ⅰ) 求函数
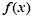 的极小值点;
的极小值点;(Ⅱ)若曲线
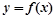 在点
在点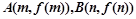 处的切线都与
处的切线都与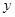 轴垂直,问是否存在常数
轴垂直,问是否存在常数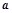 ,使函数
,使函数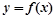 在区间
在区间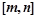 上存在零点?如果存在,求
上存在零点?如果存在,求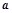 的值:如果不存在,请说明理由.
的值:如果不存在,请说明理由.(Ⅰ) 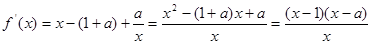
令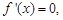 得到
得到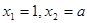 .
.
(1) 当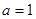 时,
时, 在定义域单调递增,没有极小值点.
在定义域单调递增,没有极小值点.
(2)当 时,当
时,当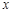 变化时,
变化时,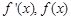 的变化情况如下表:
的变化情况如下表:
所以 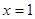 是函数的极大值点.
是函数的极大值点.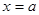 是函数的极小值点.
是函数的极小值点.
(3) 当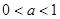 时,
时,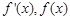 的变化情况如下表:
的变化情况如下表:
所以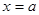 是函数的极大值点.
是函数的极大值点.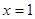 是函数的极小值点.
是函数的极小值点.
综合上述.当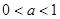 时,
时,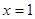 是函数的极小值点. 当
是函数的极小值点. 当 时,
时, 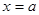 是函数的极小值点.-------6分
是函数的极小值点.-------6分
(Ⅱ)若曲线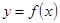 上有两点
上有两点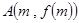 ,
,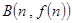 处的切线都与
处的切线都与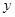 轴垂直,则
轴垂直,则 ,由(Ⅰ)的讨论知,
,由(Ⅰ)的讨论知,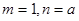 或
或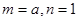 ,
,
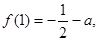 ,
, .
.
若函数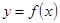 在区间
在区间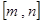 上存在零点,且单调,所以
上存在零点,且单调,所以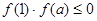 .
.
即 .所以
.所以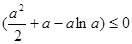 .
.
故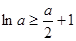 .
.
下面证明此不等式不成立.
令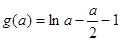 ,则
,则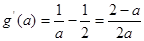 ,
,
于是当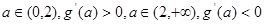 ,所以,
,所以,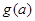 在
在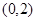 单调递增,在
单调递增,在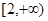 单调递减,所以函数
单调递减,所以函数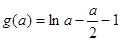 在
在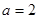 取得最大值
取得最大值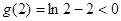 .
.
所以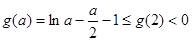 ,所以
,所以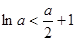 .故不存在满足要求的常数
.故不存在满足要求的常数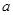 .
.
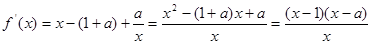
令
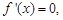 得到
得到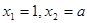 .
. (1) 当
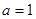 时,
时, 在定义域单调递增,没有极小值点.
在定义域单调递增,没有极小值点.(2)当
 时,当
时,当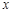 变化时,
变化时,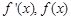 的变化情况如下表:
的变化情况如下表:  |  |  | 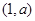 | 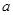 | 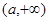 |
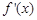 | 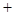 | 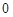 | - | 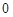 | 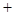 |
 |  | 极大值 |  | 极小值 |  |
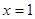 是函数的极大值点.
是函数的极大值点.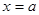 是函数的极小值点.
是函数的极小值点.(3) 当
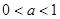 时,
时,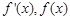 的变化情况如下表:
的变化情况如下表: 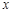 | 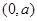 | 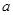 | 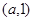 | 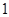 | 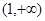 |
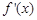 | 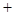 | 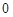 | - | 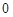 | 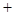 |
 |  | 极大值 |  | 极小值 |  |
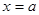 是函数的极大值点.
是函数的极大值点.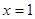 是函数的极小值点.
是函数的极小值点.综合上述.当
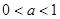 时,
时,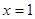 是函数的极小值点. 当
是函数的极小值点. 当 时,
时, 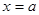 是函数的极小值点.-------6分
是函数的极小值点.-------6分(Ⅱ)若曲线
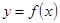 上有两点
上有两点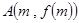 ,
,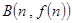 处的切线都与
处的切线都与 轴垂直,则
轴垂直,则 ,由(Ⅰ)的讨论知,
,由(Ⅰ)的讨论知,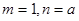 或
或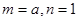 ,
,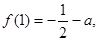 ,
, .
. 若函数
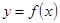 在区间
在区间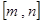 上存在零点,且单调,所以
上存在零点,且单调,所以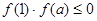 .
.即
 .所以
.所以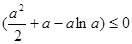 .
.故
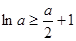 .
.下面证明此不等式不成立.
令
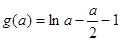 ,则
,则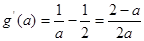 ,
,于是当
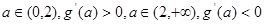 ,所以,
,所以,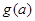 在
在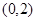 单调递增,在
单调递增,在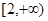 单调递减,所以函数
单调递减,所以函数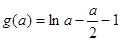 在
在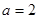 取得最大值
取得最大值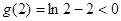 .
.所以
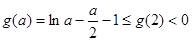 ,所以
,所以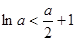 .故不存在满足要求的常数
.故不存在满足要求的常数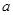 .
.略

练习册系列答案
相关题目
 到底面中心
到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
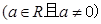 , 函数
, 函数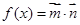 .
.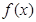 的单调区间;
的单调区间;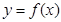 的图像在点
的图像在点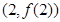 处的切线的斜率为
处的切线的斜率为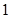 ,问:
,问: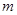 在什么范围
在什么范围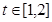 ,函数
,函数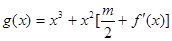 在区间
在区间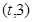 上总存在
上总存在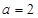 时,设函数
时,设函数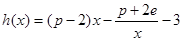 ,若在区间
,若在区间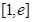 上至少存在
上至少存在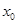 ,使得
,使得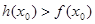 成立,试求实数
成立,试求实数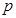 的取值范围.
的取值范围.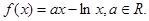
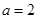 时,求曲线
时,求曲线 在点
在点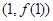 处的切线方程;
处的切线方程;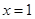 处有极值,求
处有极值,求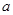 ,使
,使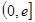 的最小值是3,若存在,求出
的最小值是3,若存在,求出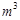 ,高为2
,高为2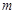 的长方体纸盒.
的长方体纸盒.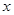 表示长方体底面一边的长,
表示长方体底面一边的长,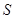 表示长方体的表面积,试写出
表示长方体的表面积,试写出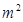 ?
?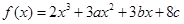 在
在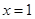 及
及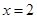 时取得极值.
时取得极值.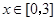 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.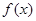 在R上满足
在R上满足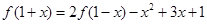 ,则曲线
,则曲线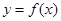 在点
在点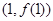 处的切线方程是 ( ▲ )
处的切线方程是 ( ▲ )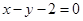
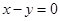
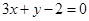
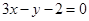
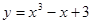 在
在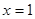 处的切线的斜率等于( )
处的切线的斜率等于( )