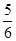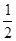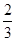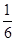题目内容
(本题满分14分) 已知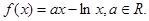
(Ⅰ)当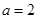 时,求曲线
时,求曲线 在点
在点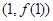 处的切线方程;
处的切线方程;
(Ⅱ)若 在
在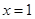 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(Ⅲ)是否存在实数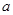 ,使
,使 在区间
在区间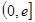 的最小值是3,若存在,求出
的最小值是3,若存在,求出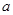 的值;
的值;
若不存在,说明理由.
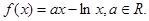
(Ⅰ)当
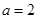 时,求曲线
时,求曲线 在点
在点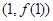 处的切线方程;
处的切线方程;(Ⅱ)若
 在
在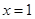 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;(Ⅲ)是否存在实数
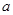 ,使
,使 在区间
在区间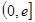 的最小值是3,若存在,求出
的最小值是3,若存在,求出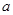 的值;
的值;若不存在,说明理由.
解:(Ⅰ)由已知得 的定义域为
的定义域为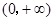 ,
,
因为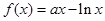 ,所以
,所以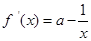
当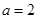 时,
时, ,所以
,所以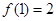 ,
,
因为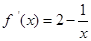 ,所以
,所以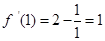 ……………………2分
……………………2分
所以曲线 在点
在点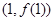 处的切线方程为
处的切线方程为
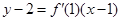 ,即
,即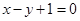 . …………………………4分
. …………………………4分
(Ⅱ)因为 在
在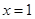 处有极值,所以
处有极值,所以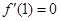 ,
,
由(Ⅰ)知 ,所以
,所以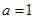
经检验,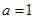 时
时 在
在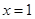 处有极值. …………………………5分
处有极值. …………………………5分
所以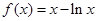 ,令
,令 解得
解得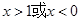 ;
;
因为 的定义域为
的定义域为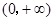 ,所以
,所以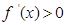 的解集为
的解集为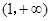 ,
,
即 的单调递增区间为
的单调递增区间为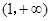 . …………………………………………8分
. …………………………………………8分
(Ⅲ)假设存在实数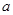 ,使
,使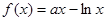 (
(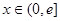 )有最小值3,
)有最小值3,
① 当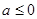 时,因为
时,因为 ,所以
,所以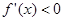 ,
,
所以 在
在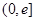 上单调递减,
上单调递减,
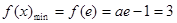 ,解得
,解得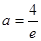 ,舍去. ……………………10分
,舍去. ……………………10分
②当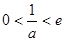 时,
时, 在
在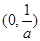 上单调递减,在
上单调递减,在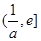 上单调递增,
上单调递增,
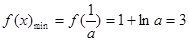 ,解得
,解得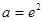 ,满足条件. …………………12分
,满足条件. …………………12分
③ 当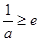 时,因为
时,因为 ,所以
,所以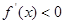 ,
,
所以 在
在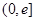 上单调递减,
上单调递减,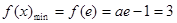 ,
,
解得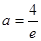 ,舍去.
,舍去.
综上,存在实数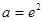 ,使得当
,使得当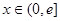 时
时 有最小值3. ……………14分
有最小值3. ……………14分
 的定义域为
的定义域为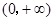 ,
,因为
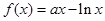 ,所以
,所以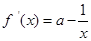
当
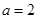 时,
时, ,所以
,所以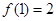 ,
,因为
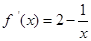 ,所以
,所以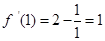 ……………………2分
……………………2分所以曲线
 在点
在点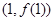 处的切线方程为
处的切线方程为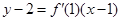 ,即
,即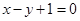 . …………………………4分
. …………………………4分(Ⅱ)因为
 在
在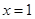 处有极值,所以
处有极值,所以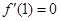 ,
,由(Ⅰ)知
 ,所以
,所以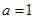
经检验,
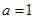 时
时 在
在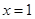 处有极值. …………………………5分
处有极值. …………………………5分所以
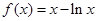 ,令
,令 解得
解得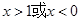 ;
;因为
 的定义域为
的定义域为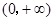 ,所以
,所以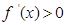 的解集为
的解集为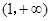 ,
,即
 的单调递增区间为
的单调递增区间为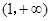 . …………………………………………8分
. …………………………………………8分(Ⅲ)假设存在实数
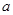 ,使
,使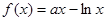 (
(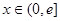 )有最小值3,
)有最小值3,① 当
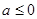 时,因为
时,因为 ,所以
,所以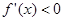 ,
,所以
 在
在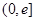 上单调递减,
上单调递减,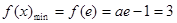 ,解得
,解得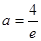 ,舍去. ……………………10分
,舍去. ……………………10分 ②当
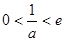 时,
时, 在
在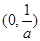 上单调递减,在
上单调递减,在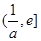 上单调递增,
上单调递增,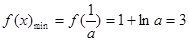 ,解得
,解得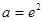 ,满足条件. …………………12分
,满足条件. …………………12分③ 当
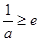 时,因为
时,因为 ,所以
,所以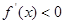 ,
,所以
 在
在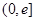 上单调递减,
上单调递减,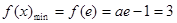 ,
,解得
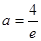 ,舍去.
,舍去.综上,存在实数
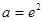 ,使得当
,使得当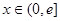 时
时 有最小值3. ……………14分
有最小值3. ……………14分略

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
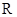 上的函数
上的函数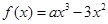 ,其中
,其中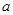 为大于零的常数.
为大于零的常数.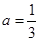 时,令
时,令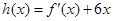 ,求证:当
,求证:当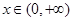 时,
时,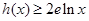 (
(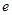 为自然对数的底数);
为自然对数的底数);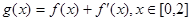 ,在
,在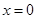 处取得最大值,求
处取得最大值,求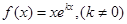
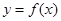 的单调性
的单调性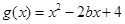 ,当k=1时,若对于任意
,当k=1时,若对于任意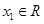 ,存在
,存在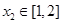
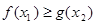 ,求实数b的取值范围
,求实数b的取值范围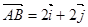 (
( 、
、 分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6. 的最小值.
的最小值.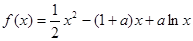 ,其中
,其中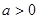 .
.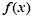 的极小值点;
的极小值点;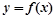 在点
在点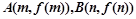 处的切线都与
处的切线都与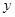 轴垂直,问是否存在常数
轴垂直,问是否存在常数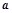 ,使函数
,使函数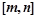 上存在零点?如果存在,求
上存在零点?如果存在,求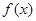 满足对一切
满足对一切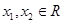 都有
都有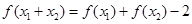 ,且
,且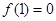 ,当
,当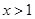 时有
时有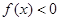 .
.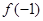 的值;
的值; 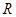 上的单调性;
上的单调性;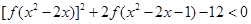
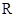 上的任意函数
上的任意函数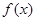 ,若满足
,若满足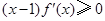 ,则必有( )
,则必有( )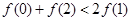
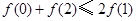
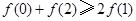
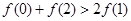
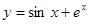 在点
在点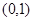 处的切线方程是
处的切线方程是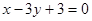
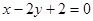
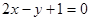

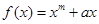 的导函数
的导函数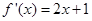 ,则
,则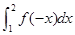 的值等于( )
的值等于( )