题目内容
若函数f(x)=
有两个不同的零点,则实数a的取值范围是 .
|
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由lnx=0,解得x=1,成立,可知存在x≤0,使2x-a=0成立,从而解实数a的取值范围.
解答:
解:令lnx=0,解得x=1,成立,
又∵函数f(x)=
有两个不同的零点,
∴存在x≤0,使2x-a=0成立,
即a=2x≤0,
故答案为:(-∞,0].
又∵函数f(x)=
|
∴存在x≤0,使2x-a=0成立,
即a=2x≤0,
故答案为:(-∞,0].
点评:本题考查了函数的零点与方程的根之间的关系,属于基础题.

练习册系列答案
相关题目
对于连续不间断的函数y=f(x),定义面积函数y=∫
f(x)为直线x=a,x=b,y=0与y=f(x)围成的图形的面积,则∫
x+∫
(2x-4)-∫
log2x的值为( )
b a |
4 0 |
2 0 |
4 1 |
| A、6 | B、8 | C、9 | D、10 |
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的一段图象如下,则f(x)的解析式为( )
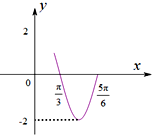

A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(2x-
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(2x-
|
已知双曲线
-
=1的一个焦点与圆x2+y2-2x=0的圆心重合,且双曲线的离心率等于
,则该双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、5x2-
| ||||
B、
| ||||
C、
| ||||
D、5y2-
|
设函数f(x)=xlnx,则( )
| A、x=1为f(x)的极大值点 | ||
| B、x=1为f(x)的极小值点 | ||
C、x=
| ||
D、x=
|
连续函数y=f(x)在点x0取极值是f′(x0)=0的( )
| A、充分条件 | B、必要条件 |
| C、充要条件 | D、必要非充分条件 |