题目内容
一条光线从点P（1，1）发出，先经x轴反射，又经y轴反射后过点Q（2，3），则光线从点P到点Q所经过的路程为（ ）
A、
| ||
| B、5 | ||
C、
| ||
D、
|
考点：与直线关于点、直线对称的直线方程
专题：直线与圆
分析：如图所示，根据反射定律可得P′、M、N、Q′在通一条直线上，且PM=P′M，NQ=N′Q，光线从点P到点Q所经过的路程为PM+MN+NQ=P′Q′，计算求得结果．
解答：
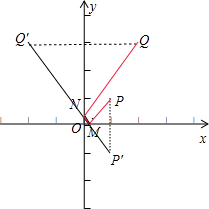解：设光线与x轴的交点为M，与y轴的交点为N，
再设点P（1，1）关于x轴的对称点为P′（1，-1），
点Q（2，3）关于y轴的对称点Q′（-2，3），
则由反射定理可得P′、M、N、Q′在通一条直线上，
PM=P′M，NQ=N′Q，
故光线从点P到点Q所经过的路程为PM+MN+NQ=P′Q′=5，
故选：B．
解：设光线与x轴的交点为M，与y轴的交点为N，再设点P（1，1）关于x轴的对称点为P′（1，-1），
点Q（2，3）关于y轴的对称点Q′（-2，3），
则由反射定理可得P′、M、N、Q′在通一条直线上，
PM=P′M，NQ=N′Q，
故光线从点P到点Q所经过的路程为PM+MN+NQ=P′Q′=5，
故选：B．
点评：本题主要考查反射定律的应用、求点关于直线的对称点，体现了转化、数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
一个样本的容量为60，分成5组，已知第一组、第三组的频数分别是9、10，第二、五组的频率都为
，则该样本的中位数在（ ）
| 1 |
| 5 |
| A、第二组 | B、第三组 |
| C、第四组 | D、第五组 |