题目内容
11.正△ABC中,过其中心G作边BC的平行线,分别交AB,AC于点B1,C1,将△AB1C1沿B1C1折起到△A1B1C1的位置,使点A1在平面BB1C1C上的射影恰是线段BC的中点M,则二面角A1-B1C1-M的平面角大小是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 连接A1G,MG,由G为三角形ABC的中心可得B1C1⊥A1G,GM⊥B1C1,故而∠A1GM为二面角A1-B1C1-M的平面角,在Rt△A1GM中,根据A1G和GM的数量关系得出∠A1GM.
解答 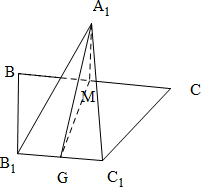 解:连接A1G,MG,
解:连接A1G,MG,
∵G是正三角形ABC的中心,B1C1∥BC,
∴B1C1⊥A1G,GM⊥B1C1,
∴∠A1GM为二面角A1-B1C1-M的平面角,
∵G是正三角形ABC的中心,
∴A1G=2GM,
又A1M⊥平面BB1C1C,
∴cos∠A1GM=$\frac{GM}{{A}_{1}G}$=$\frac{1}{2}$,
∴∠A1GM=$\frac{π}{3}$.
故选C.
点评 本题考查了二面角的计算,作出二面角的平面角是关键,属于中档题.

练习册系列答案
相关题目
2.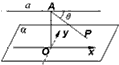 如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )
如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )
 如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )
如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )| A. | tan2θx2+y2=d2 | B. | tan2θx2-y2=d2 | C. | ${y^2}=2d(x-\frac{d}{tanθ})$ | D. | ${y^2}=-2d(x-\frac{d}{tanθ})$ |
1.2位女生和3位男生共5位同学站成一排,若女生甲不站两端,3位男生中有且只有两位男生相邻,则不同排法的种数是( )
| A. | 36 | B. | 42 | C. | 48 | D. | 60 |
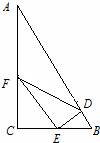 某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米,现在准备养一批供游客观赏的鱼,分别在AB,BC,CA上取点D,E,F,如图,使得EF∥AB,EF⊥ED,在△DEF喂食,求S△DEF的最大值.