题目内容
10.已知函数f(x)=3sin(${\frac{1}{2}x+\frac{π}{6}}$),(1)若点P(1,-$\sqrt{3}$)在角α的终边上,求$f(2α-\frac{π}{3})$的值;
(2)若x∈[-$\frac{2π}{3}$,$\frac{4π}{3}$],求f(x)的值域.
分析 (1)由条件利用任意角的三角函数的定义求得sinα的值,可得f(2α-$\frac{π}{3}$)的值.
(2)利用正弦函数的定义域和值域,求得f(x)的值域.
解答 解:(1)∵函数f(x)=3sin(${\frac{1}{2}x+\frac{π}{6}}$),点$P(1,-\sqrt{3})$在角α的终边上,∴$sinα=\frac{{-\sqrt{3}}}{{\sqrt{{1^2}+{{(-\sqrt{3})}^2}}}}=-\frac{{\sqrt{3}}}{2}$,∴f(2α-$\frac{π}{3}$)=3sin(α-$\frac{π}{6}$+$\frac{π}{6}$)=3sinα=-$\frac{3\sqrt{3}}{2}$.
(2)∵$x∈[-\frac{2π}{3},\frac{4π}{3}]$,∴$\frac{1}{2}x+\frac{π}{6}∈[-\frac{π}{6},\frac{5π}{6}]$,∴$-\frac{1}{2}≤sin(\frac{1}{2}x+\frac{π}{6})≤1$,
∴$-\frac{3}{2}≤3sin(\frac{1}{2}x+\frac{π}{6})≤3$,即 函数的值域为$[-\frac{3}{2},3]$.
点评 本题主要考查任意角的三角函数的定义,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
20.已知函数f(x)在R上可导,其部分图象如图所示,设$\frac{f(2)-f(1)}{2-1}$=a,则下列不等式正确的是( )

| A. | f′(1)<f′(2)<a | B. | f′(1)<a<f′(2) | C. | f′(2)<f′(1)<a | D. | a<f′(1)<f′(2) |
18.若${\vec e_1}$,${\vec e_2}$是夹角为60°的两个单位向量,则$\vec a$=2${\vec e_1}$+${\vec e_2}$;$\vec b$=-3${\vec e_1}$+2${\vec e_2}$的夹角为( )
| A. | 60° | B. | 30° | C. | 150° | D. | 120° |
20.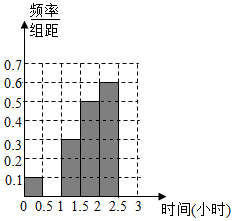 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.
(1)确定x,y,p,q的值,并补全须率分布直方图;
(2)为进一步了解使用微信对自己的日不工作和生活是否有影响,从“微信达人”和“非微信达人”60人中用分层抽样的方法确定10人,若需从这10人中随积选取3人进行问卷调查,设选取的3人中“微信达人”的人数为X,求X的分布列和数学期望.
 微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.
微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2.(1)确定x,y,p,q的值,并补全须率分布直方图;
(2)为进一步了解使用微信对自己的日不工作和生活是否有影响,从“微信达人”和“非微信达人”60人中用分层抽样的方法确定10人,若需从这10人中随积选取3人进行问卷调查,设选取的3人中“微信达人”的人数为X,求X的分布列和数学期望.
| 使用微信时间(单位:小时) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
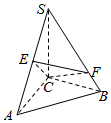 直线SC⊥面ABC,AB⊥BC,且AB=BC=1,SA=2,E为SA中点,F为点C在线BS上的射影.
直线SC⊥面ABC,AB⊥BC,且AB=BC=1,SA=2,E为SA中点,F为点C在线BS上的射影.