题目内容
10.设集合S={x|x>-2},T={x|x2+3x-4≤0},则(∁RS)∪T={x|x≤1}.分析 先根据一元二次不等式求出集合T,然后求得∁RS,再利用并集的定义求出结果.
解答 解:∵集合S={x|x>-2},
∴∁RS={x|x≤-2},
T={x|x2+3x-4≤0}={x|-4≤x≤1},
故(∁RS)∪T={x|x≤1},
故答案为:{x|x≤1}.
点评 此题属于以一元二次不等式的解法为平台,考查了补集及并集的运算,是高考中常考的题型.在求补集时注意全集的范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在△ABC中,角A、B、C所对的边分别为a,b,c若2acosB=c,则2cos2$\frac{A}{2}$+sinB-1的取值范围是 ( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | (-1,$\sqrt{2}$] |
18.在△ABC中,若sinA>sinB,则A与B的大小关系为( )
| A. | A、B的大小关系不确定 | B. | A=B | ||
| C. | A<B | D. | A>B |
19.比较a=2-3.1,b=0.53,c=log3.14,则a,b,c的大小关系是( )
| A. | c<b<a | B. | b<c<a | C. | a<c<b | D. | a<b<c |
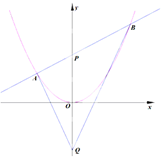 如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.
如图所示,过抛物线C:x2=4y的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是点P关于原点的对称点.