题目内容
5.设y=f(x)是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1(1)求f(x)的解析式
(2)求函数y=log3f(x)的值域.
分析 (1)设f(x)=ax2+bx+c,由f(0)=8可求c,由f(x+1)-f(x)=-2x+1可构造关于a,b的方程组,可求解.
(2)结合对数函数的单调性以及一元二次函数的性质进行求解即可.
解答 解:(1)设f(x)=ax2+bx+c,
∵f(0)=8,∴c=8
又f(x+1)=a(x+1)2+b(x+1)+c,
∵f(x+1)-f(x)=-2x+1
∴a(x+1)2+b(x+1)+c-(ax2+bx+c)=2ax+a+b=-2x+1,
∴$\left\{\begin{array}{l}2a=-2\\ a+b=1\end{array}\right.$,
∴a=-1,b=2
∴f(x)=-x2+2x+8.
(2)∵f(x)=-x2+2x+8=-(x-1)2+9,
∴由y=log3f(x)得0<f(x)≤9,
则y=log3f(x)≤log39=2,
即函数的值域为(-∞,2].
点评 本题主要考查函数解析式以及函数值域的求解,根据一元二次函数的性质,利用待定系数法是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设M={1,2,3,4,5,6,7,8,9,10},由M到M上的一一映射中,有7个数字和自身对应的映射个数是( )
| A. | 120 | B. | 240 | C. | 107 | D. | 360 |
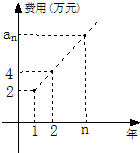 某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.