题目内容
4.在△ABC中,A=$\frac{π}{3}$,a=$\sqrt{3}$,则BC边上的中线AM长的取值范围是($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$].分析 分别在△ABM中和△ABM中应用余弦定理可得AM2=$\frac{A{B}^{2}+A{C}^{2}}{2}$-$\frac{3}{4}$,再在△ABC中由余弦定理和基本不等式可得3<AB2+AC2≤6,由不等式的性质可得.
解答 解:∵在△ABC中A=$\frac{π}{3}$,a=$\sqrt{3}$,且BC边上的中线为AM,∴BM=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$,
在△ABM中由余弦定理可得AB2=$\frac{3}{4}$+AM2-2×$\frac{\sqrt{3}}{2}$×AM×cos∠AMB,①
同理在△ABM中由余弦定理可得AC2=$\frac{3}{4}$+AM2-2×$\frac{\sqrt{3}}{2}$×AM×cos∠AMC=$\frac{3}{4}$+AM2+2×$\frac{\sqrt{3}}{2}$×AM×cos∠AMB,②
①+②可得AM2=$\frac{A{B}^{2}+A{C}^{2}}{2}$-$\frac{3}{4}$,在△ABC中由余弦定理可得3=AB2+AC2-2•AB•ACcosA=AB2+AC2-AB•AC,
故AB2+AC2=3+AB•AC>3,再由基本不等式可得3=AB2+AC2-AB•AC≥AB2+AC2-$\frac{1}{2}$(AB2+AC2),
∴3<AB2+AC2≤6,故$\frac{3}{2}$<$\frac{A{B}^{2}+A{C}^{2}}{2}$≤3,∴$\frac{3}{4}$<$\frac{A{B}^{2}+A{C}^{2}}{2}$-$\frac{3}{4}$≤$\frac{9}{4}$,∴AM∈($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$],
故答案为:($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$].
点评 本题考查解三角形,涉及余弦定理和基本不等式求值域,整体求解是解决问题的关键,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | [$\sqrt{3}$,1+$\frac{\sqrt{3}}{2}$] | B. | [-$\frac{\sqrt{3}}{2}$,1-$\frac{\sqrt{3}}{2}$] | C. | [0,1] | D. | [-$\sqrt{3}$,1-$\frac{\sqrt{3}}{2}$] |
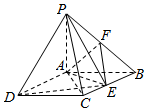 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.
如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.