题目内容
定义域为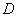 的函数
的函数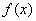 ,如果对于区间
,如果对于区间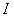 内
内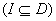 的任意两个数
的任意两个数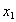 、
、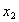 都有
都有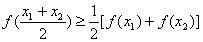 成立,则称此函数在区间
成立,则称此函数在区间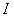 上是“凸函数”.
上是“凸函数”.
(1)判断函数 在
在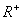 上是否是“凸函数”,并证明你的结论;
上是否是“凸函数”,并证明你的结论;
(2)如果函数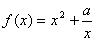 在
在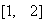 上是“凸函数”,求实数
上是“凸函数”,求实数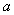 的取值范围;
的取值范围;
(3)对于区间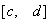 上的“凸函数”
上的“凸函数”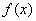 ,在
,在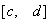 上任取
上任取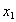 ,
,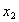 ,
, ,……,
,……,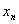 .
.
① 证明:当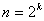 (
(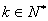 )时,
)时,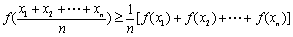 成立;
成立;
② 请再选一个与①不同的且大于1的整数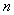 ,
,
证明: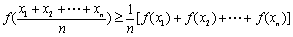 也成立.
也成立.
解:(1)设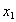 ,
,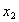 是
是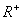 上的任意两个数,则
上的任意两个数,则


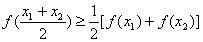 .
. 函数
函数 在
在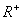 上是 “凸函数”.
上是 “凸函数”.
(2)对于 上的任意两个数
上的任意两个数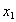 ,
,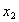 ,均有
,均有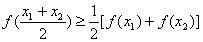 成立,即
成立,即 ,整理得
,整理得

若 ,
,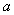 可以取任意值.
可以取任意值.
若 ,得
,得 ,
,
 ,
,
 .
.
综上所述得 .
.
(3)①当 时由已知得
时由已知得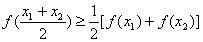 成立.
成立.
假设当
 时,不等式成立即
时,不等式成立即
 成立.
成立.
那么,由 ,
,
得


 .
.
即 时,不等式也成立.根据数学归纳法原理不等式得证.
时,不等式也成立.根据数学归纳法原理不等式得证.
②比如证明 不等式成立.由①知
不等式成立.由①知 ,
, ,
, ,
, ,
,
有 成立.
成立.

 ,
, ,
, ,
, ,
,


 ,
,
从而得 .
.

练习册系列答案
相关题目
 的定义域为集合
的定义域为集合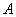 ,函数
,函数 的定义域为集合
的定义域为集合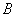 .若
.若 ,求实数
,求实数 的取值范围.
的取值范围. 的棱长是3,点
的棱长是3,点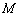 、
、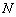 分别是棱
分别是棱 、
、 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小等于 .
所成角的大小等于 . 的棱上到异面直线
的棱上到异面直线 ,
, 的距离相等的点的个数为( )
的距离相等的点的个数为( ) 2
2  3
3  4
4  5
5  中,角
中,角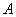 ,
, ,
, 所对的边长分别为
所对的边长分别为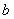 ,,向量
,,向量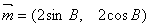 ,
,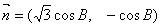 ,且
,且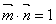 .
.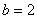 ,求
,求 满足
满足 ,则复数
,则复数 是半径为
是半径为 的球面上的四个不同点,且满足
的球面上的四个不同点,且满足 ,
, ,
, ,用
,用 分别表示△
分别表示△ 、△
、△ 、△
、△ 的面积,则
的面积,则 的最大值是 .
的最大值是 .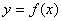 的定义域为
的定义域为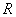 ,若存在常数
,若存在常数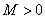 ,使得
,使得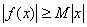 对一切实数
对一切实数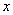
 均成立,则称
均成立,则称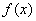 为“圆锥托底型”函数.
为“圆锥托底型”函数.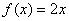 ,
,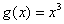 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.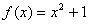 是“圆锥托底型”函数,求出
是“圆锥托底型”函数,求出 的最大值.
的最大值. 的二项展开式中含
的二项展开式中含 项的系数为
项的系数为 ,则
,则 _________.
_________.