题目内容
函数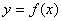 的定义域为
的定义域为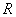 ,若存在常数
,若存在常数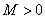 ,使得
,使得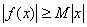 对一切实数
对一切实数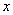
 均成立,则称
均成立,则称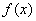 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数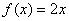 ,
,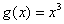 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若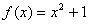 是“圆锥托底型”函数,求出
是“圆锥托底型”函数,求出 的最大值.
的最大值.
(1). ,即对于一切实数
,即对于一切实数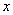 使得
使得 成立,
成立,
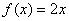 “圆锥托底型”函数.对于
“圆锥托底型”函数.对于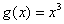 ,如果存在
,如果存在 满足
满足 ,而当
,而当 时,由
时,由 ,
,

 ,得
,得 ,矛盾,
,矛盾,
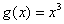 不是“圆锥托底型”函数.
不是“圆锥托底型”函数.
(2)
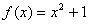 是“圆锥托底型” 函数,故存在
是“圆锥托底型” 函数,故存在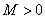 ,使得
,使得 对于任意实数恒成立.
对于任意实数恒成立.
 当
当 时,
时, ,此时当
,此时当 时,
时, 取得最小值2,
取得最小值2,
 .
. 而当
而当 时,
时, 也成立.
也成立.
 的最大值等于
的最大值等于 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
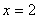 与双曲线
与双曲线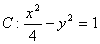 的渐近线交于
的渐近线交于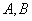 两点,设
两点,设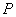 为双曲线
为双曲线 上的任意一点,若
上的任意一点,若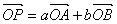 (
(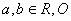 为坐标原点),则下列不等式恒成立的是( )
为坐标原点),则下列不等式恒成立的是( )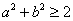 B.
B.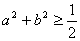
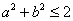 D.
D.
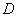 的函数
的函数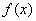 ,如果对于区间
,如果对于区间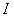 内
内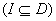 的任意两个数
的任意两个数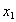 、
、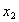 都有
都有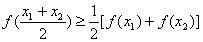 成立,则称此函数在区间
成立,则称此函数在区间 在
在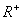 上是否是“凸函数”,并证明你的结论;
上是否是“凸函数”,并证明你的结论;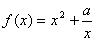 在
在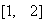 上是“凸函数”,求实数
上是“凸函数”,求实数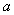 的取值范围;
的取值范围;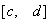 上的“凸函数”
上的“凸函数” ,……,
,……,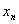 .
.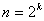 (
(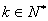 )时,
)时,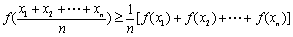 成立;
成立;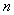 ,
, ,则
,则 且
且
 中,
中, 是
是 的充要条件
的充要条件 ,则
,则
 ,则
,则 ”的否命题是“若
”的否命题是“若 ,则
,则 ”
”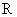 中,我们定义的大小关系“
中,我们定义的大小关系“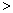 ”为全体实数排了一个“序”.类似的,我们在复数集
”为全体实数排了一个“序”.类似的,我们在复数集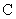 上也可以定义一个称为“序”的关系,记为“
上也可以定义一个称为“序”的关系,记为“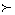 ”.定义如下:对于任意两个复数
”.定义如下:对于任意两个复数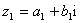 ,
,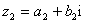 (
(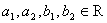 ),
),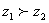 当且仅当“
当且仅当“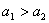 ”或“
”或“ 且
且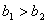 ”.
”.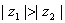 ;
;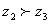 ,则
,则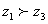 ;
;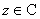 ,
,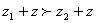 ;
;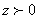 ,若
,若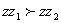 .
.
 ,侧面积为
,侧面积为
 ,则此圆锥的体积为________
,则此圆锥的体积为________ .
. ,
, ,则“
,则“ ∥
∥ ”是“
”是“ ”的( )
”的( ) 作直线l交x轴于A点、交y轴于B点,且P位于AB两点之间.
作直线l交x轴于A点、交y轴于B点,且P位于AB两点之间. ,求直线l的方程;
,求直线l的方程; 取得最小值时直线l的方程.
取得最小值时直线l的方程.