题目内容
2．复数z=$\frac{（i-1）^{2}+4}{i+1}$的虚部为（ ）| A． | -1 | B． | -3 | C． | 1 | D． | 2 |
分析 直接利用复数代数形式的乘除运算化简得答案．
解答 解：∵z=$\frac{（i-1）^{2}+4}{i+1}$=$\frac{-2i+4}{1+i}=\frac{（4-2i）（1-i）}{（1+i）（1-i）}=\frac{2-6i}{2}=1-3i$，
∴复数z=$\frac{（i-1）^{2}+4}{i+1}$的虚部为-3．
故选：B．
点评 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．
练习册系列答案
相关题目
15．设△ABC的内角A、B、C的对边分别为a、b、c，若a=1，c=$\sqrt{3}$，cosA=$\frac{\sqrt{3}}{2}$，且b＜c，则b=（ ）
| A． | 1 | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
13．
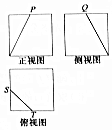一个几何体的三视图是如图所示的边长为2的正方形，其中P，Q，S，T为各边的中点，则此几何体的表面积是（ ）
一个几何体的三视图是如图所示的边长为2的正方形，其中P，Q，S，T为各边的中点，则此几何体的表面积是（ ）| A． | 21 | B． | $\frac{43}{2}$ | C． | $\frac{45}{2}$ | D． | 23 |
7．已知x∈（0，π），且cos（2x-$\frac{π}{2}$）=sin2x，则tan（x-$\frac{π}{4}$）等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |
我们把离心率e=$\frac{\sqrt{5}+1}{2}$的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）称为黄金双曲线．如图是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0，c=$\sqrt{{a}^{2}+{b}^{2}}$）的图象，给出以下几个说法：