题目内容
在10件产品中有2件次品,连续抽3次,每次抽1件,抽后不放回,则至少抽到1件次品的概率为 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:本题是一个等可能事件的概率,试验发生所包含的事件是从10件产品中抽取3件,共有C103=120种结果,3次抽取中一1件次品也没有抽到的有C83=56,至少抽到1件次品为120-56=64,则得到概率.
解答:
解:试验发生所包含的事件是从10件产品中抽取3件,共有C103=120种结果,
3次抽取中一1件次品也没有抽到的有C83=56,
则至少抽到1件次品为120-56=64,
故3至少抽到1件次品的概率P=
=
.
故答案为:
.
3次抽取中一1件次品也没有抽到的有C83=56,
则至少抽到1件次品为120-56=64,
故3至少抽到1件次品的概率P=
| 64 |
| 120 |
| 8 |
| 15 |
故答案为:
| 8 |
| 15 |
点评:本题考查等可能事件的概率,可以应用穷举法,列举是基本的解题方法,注意不要重复、不要遗漏.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
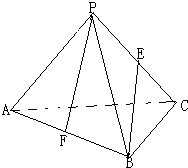 如图,在正四面体PABC中,若E,F分别是PC,AB的中点,则异面直线PF与BE所成的角的余弦值为
如图,在正四面体PABC中,若E,F分别是PC,AB的中点,则异面直线PF与BE所成的角的余弦值为