题目内容
数列1,2,4,8,16,32,…的一个通项公式是( )
| A.an=2n-1 | B.an= | C.an= | D.an= |
B
解析试题分析:观察此数列是首项是1,且是公比为2的等比数列,根据等比数列的通项公式求出此数列 的一个通项公式.
由于数列1,2,4,8,16,32,…的第一项是1,且是公比为2的等比数列,
故通项公式是 ,故此数列的一个通项公式
,故此数列的一个通项公式 ,
,
故选B.
考点:数列的通项公式
点评:根据数列的前几项归纳猜想其通项公式,这是数列的特点,就是猜想,注意找数字的与项的关系,得到结论。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果数列 的前
的前 项和
项和 ,那么这个数列的通项公式是 ( )
,那么这个数列的通项公式是 ( )
A. | B. |
C. | D.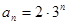 |
在各项均为正数的数列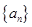 中,对任意
中,对任意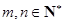 都有
都有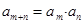 .若
.若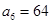 ,
,
则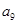 等于( )
等于( )
| A.256 | B.510 | C.512 | D.1024 |
已知数列 是公差为
是公差为 的等差数列,且
的等差数列,且 成等比数列,则
成等比数列,则 的前
的前 项和
项和 为( )
为( )
A. | B. | C. | D. |
数列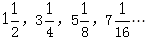 的前
的前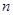 项和为 ( )
项和为 ( )
A.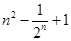 | B.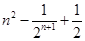 |
C.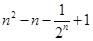 | D.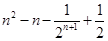 |
已知数列 满足
满足 若
若 则
则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
已知
 则当
则当 时,n的最小值是
时,n的最小值是
| A.9 | B.10 | C.11 | D.12 |
 ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.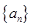 的前
的前 项和为
项和为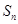 ,且
,且 ,则
,则 .
.